1 Introduction
L’épure de Méry permet d’évaluer la stabilité d’une voûte en berceau en quelques étapes simples de dessin. Nous introduirons l’épure par un exemple pratique dans la première partie de cet article. Cette exemple ne nécessite pas de prérequis particuliers sur la stabilité des voûtes. Il permet de prendre en main de façon concrète la méthode. Il est possible qu’à la fin de cette première partie, le lecteur trouve que notre présentation ne correspond pas à ce qu’il connaît de l’épure de Méry. La raison est simple : la méthode publiée par Méry en 1840 est modifiée progressivement au XIXe siècle. Différentes simplifications y sont apportés, sans pour autant entraîner de changement du nom de la méthode, qui continue à être appelée épure de Méry, méthode de Méry ou règle de Méry. L’expression méthode des courbes des pressions hypothétiques est plus rarement employé pour désigner la méthode de Méry. Nous proposons donc un article à plusieurs niveaux de lecture. La première partie, qui présente de façon concrète l’application de l’épure de Méry intéressera les lecteurs qui ne sont pas familiers avec cette dernière. La seconde partie présente une synthèse du mémoire de Méry de 1840, puis les modifications de la méthode de la seconde moitié du XIXe siècle. Cette partie permettra aux lecteurs qui connaissent déjà l’épure de Méry sous une forme différente, de situer leur pratique par rapport à l’épure de Méry d’origine. Nous verrons ensuite l’évolution de cette méthode d’un point de vue historique. Nous chercherons enfin à comprendre l’origine du succès de cette méthode, par rapport à la construction des polygones funiculaires à l’aide de la statique graphique.2 Prise en main de l’épure de Méry
2.1 Contexte
Méry est un ingénieur des Ponts et Chaussées, qui publie en 1840 un mémoire qui va connaître un grand succès : Sur l’équilibre des voûtes en berceau ([14]). Ce mémoire marque l’aboutissement d’un travail commencé1 en 1826-1827. Méry donne en introduction à son mémoire une synthèse claire de son objectif :Cette construction géométrique est la ligne de pression, qui représente la suite des points d’application des résultantes des forces (ou pressions) sur les joints. Méry appelle cette ligne alternativement courbe de pression, ou courbe des pressions. Nous allons voir pour commencer le moyen donné par Méry pour construire les courbes de pression que nous appelons aujourd’hui lignes de pression en France. Nous reviendrons ultérieurement plus amplement sur les propriétés de ces lignes de pression, notons simplement pour le moment que l’existence d’une ligne de pression comprise à l’intérieur de la maçonnerie prouve la possibilité d’équilibre de la voûte étudiée.Nous nous proposons de donner le moyen de vérifier la stabilité des voûtes par une construction géométrique qui dispense de tout calcul, et dont nous avons constaté la simplicité par de fréquentes applications. Méry 1840 [14,p.50]
2.2 Construction de la courbe de pression – Cas 1
La première question à laquelle répond Méry par son mémoire est la suivante : comment tracer la courbe de pression d’une voûte en berceau symétrique qui passe en deux points connus. Nous reprenons la figure 4 de la planche CLXXXIII du mémoire de Méry, et nous allons présenter étape par étape la construction de la courbe de pression. Pour faciliter les références que nous ferons ultérieurement à cette construction, nous appellerons ce premier cas donné par Méry Cas 1. Problème de départ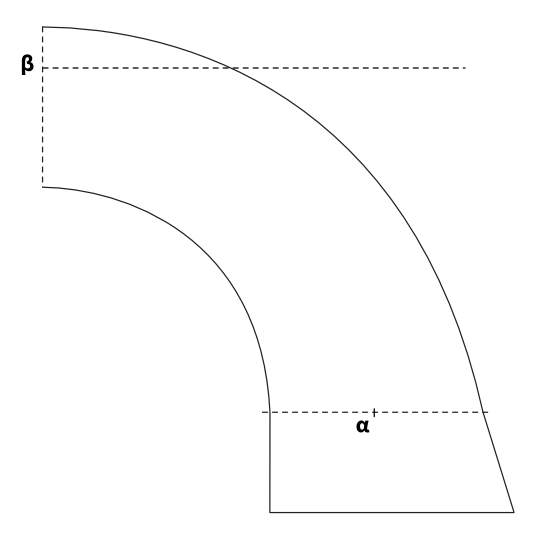 Méry choisit deux points arbitraires $\alpha $ et $\beta $ positionnés respectivement en pied et en tête de la voûte.
Il trace l’horizontale passant par le point $\beta $.
Première étape
Méry choisit deux points arbitraires $\alpha $ et $\beta $ positionnés respectivement en pied et en tête de la voûte.
Il trace l’horizontale passant par le point $\beta $.
Première étape  Méry considère dans un premier temps la portion de voûte comprise entre $\alpha $ et $\beta $, que nous avons représenté en bleu ci-contre. Il trace la verticale $KG$ passant par le centre de gravité de la partie bleue, avec le point $K$ placé sur l’horizontale passant par $\beta $.
Méry place ensuite sur cette verticale le vecteur $KS$ proportionnel au poids de la portion de voûte considérée (en bleu). Enfin, il trace la ligne passant par les points $\alpha $ et $K$.
Deuxième étape
Méry considère dans un premier temps la portion de voûte comprise entre $\alpha $ et $\beta $, que nous avons représenté en bleu ci-contre. Il trace la verticale $KG$ passant par le centre de gravité de la partie bleue, avec le point $K$ placé sur l’horizontale passant par $\beta $.
Méry place ensuite sur cette verticale le vecteur $KS$ proportionnel au poids de la portion de voûte considérée (en bleu). Enfin, il trace la ligne passant par les points $\alpha $ et $K$.
Deuxième étape  Méry projette horizontalement le point $S$ sur la droite passant par $\alpha $, ce qui donne le point $R$, puis obtient par projection verticale le point $P$.
Il obtient ainsi graphiquement la poussée horizontale $KP$, et la force oblique $KR$ qui s’appliquent en pied de la voûte au point $\alpha $, pour ce choix arbitraire de points $\alpha $ et $\beta $.
Troisième étape
Méry projette horizontalement le point $S$ sur la droite passant par $\alpha $, ce qui donne le point $R$, puis obtient par projection verticale le point $P$.
Il obtient ainsi graphiquement la poussée horizontale $KP$, et la force oblique $KR$ qui s’appliquent en pied de la voûte au point $\alpha $, pour ce choix arbitraire de points $\alpha $ et $\beta $.
Troisième étape 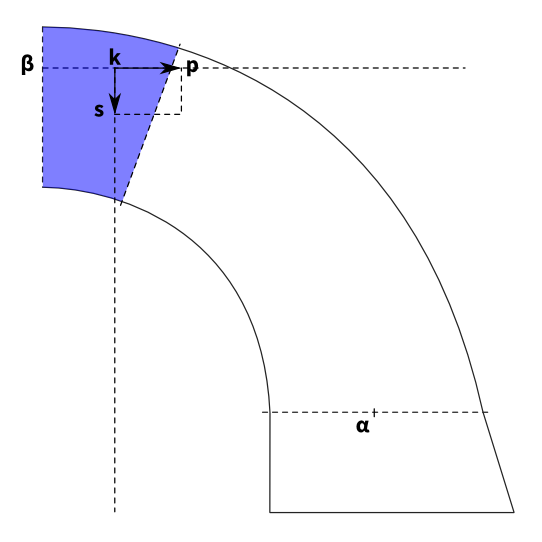 Méry cherche alors le point de passage de la courbe de pression par un joint situé près de la clé. Il reprend alors la même construction que précédemment : tracer la verticale passant par le centre de gravité de la portion de voûte comprise entre la clé et le joint considéré (en bleu ici), tracer le vecteur $ks$ représentant le poids de la portion de voûte. De plus, la poussée de la courbe de pression est connue, et il trace alors $kp$ = $KP$
Quatrième étape
Méry cherche alors le point de passage de la courbe de pression par un joint situé près de la clé. Il reprend alors la même construction que précédemment : tracer la verticale passant par le centre de gravité de la portion de voûte comprise entre la clé et le joint considéré (en bleu ici), tracer le vecteur $ks$ représentant le poids de la portion de voûte. De plus, la poussée de la courbe de pression est connue, et il trace alors $kp$ = $KP$
Quatrième étape 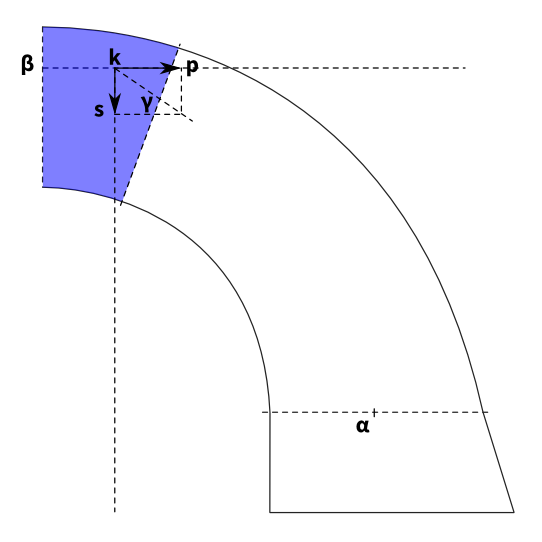 La position du centre de pression $\gamma $ est donné par l’intersection entre le joint considéré et la diagonale du rectangle formé par $ks$ et $kp$.
Cinquième étape
La position du centre de pression $\gamma $ est donné par l’intersection entre le joint considéré et la diagonale du rectangle formé par $ks$ et $kp$.
Cinquième étape 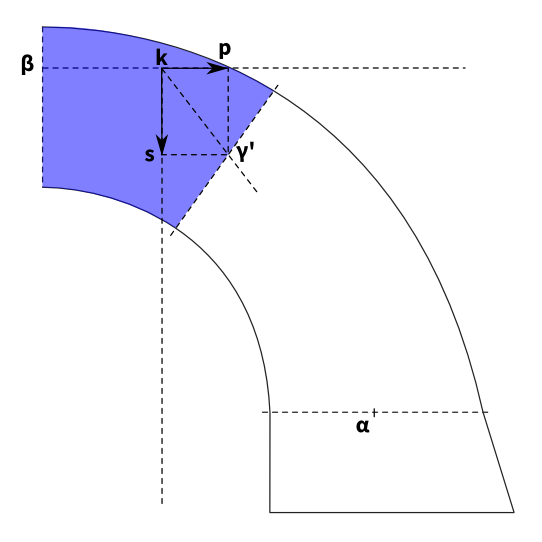 La troisième et quatrième étape sont alors répétées en chaque joint de la voûte où l’on souhaite obtenir le point passage de la courbe de pression. Ici un autre point de passage $\gamma’$ sur un joint situé un peu plus bas que le joint précédent.
Résultat
La troisième et quatrième étape sont alors répétées en chaque joint de la voûte où l’on souhaite obtenir le point passage de la courbe de pression. Ici un autre point de passage $\gamma’$ sur un joint situé un peu plus bas que le joint précédent.
Résultat 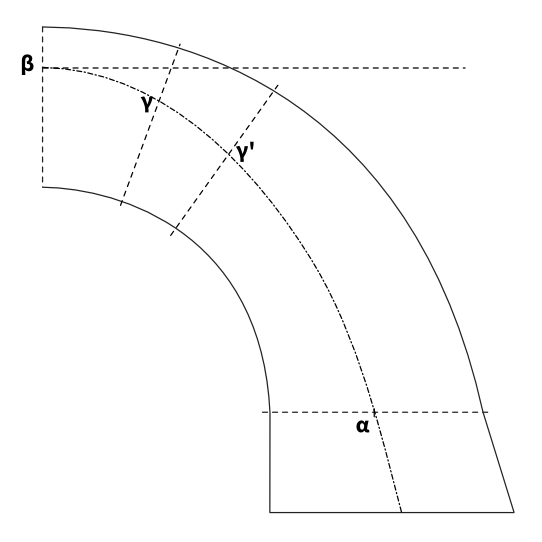 La répétition de ces quelques dessins simples permet de construire de proche en proche la ligne de pression passant par $\alpha $ et $\beta $.
La répétition de ces quelques dessins simples permet de construire de proche en proche la ligne de pression passant par $\alpha $ et $\beta $.
2.3 Construction de la courbe de pression – Cas 2
La méthode de construction donnée ci-dessus ne s’applique que si le point $\beta $ est situé sur la clé de voûte. Méry donne également une méthode de construction de la ligne de pression, si le point $\beta $ n’est pas situé sur la clé de voûte. Cette seconde méthode est moins connue. Elle n’est par exemple pas reproduite dans les différents traités de construction du XIXe que nous citerons par la suite. Son application n’est pas plus complexe, mais elle a été beaucoup moins utilisée. Nous ne la détaillerons pas ici. Notons simplement au passage une coquille dans le mémoire d’origine, qui a pu gêner la compréhension et la diffusion de cette construction : il faut lire $\frac{1}{mt}:\frac{1}{M\alpha }$ et non $\frac{1}{mt}:\frac{1}{m\alpha }$ sur l’équation de la page 53, les points $M$ et $m$ étant distincts. Pour faciliter les références que nous ferons ultérieurement à cette construction, nous appellerons ce second cas donné par Méry Cas 2.2.4 Recherche de la poussée minimum et maximum
Grâce à sa méthode, Méry nous permet donc de construire toute ligne de pression en faisant au préalable une hypothèse sur la position de deux points de passage de la ligne de pression recherchée. Comment choisir alors ces points de passages ? Méry indique qu’il suffit en pratique de rechercher les lignes de pression de poussées extrémales, c’est-à-dire la poussée maximum ou la poussée minimum pour lesquelles la voûte peut-être stable. Il remarque que les lignes de pression de poussée minimum et maximum, ces lignes touchent l’intrados et l’extrados dans des zones que l’on connaît par expérience, et qui sont donc de bonnes premières hypothèses pour débuter les étapes de dessins. Il propose donc de :- faire une hypothèse sur la position où la ligne de pression devrait toucher l’intrados et l’extrados
- de choisir deux points $\alpha $ et $\beta $ grâce à cette hypothèse
- de dessiner la ligne de pression correspondante
- de vérifier que cette ligne de pression est bien incluse entièrement dans la voûte, et sinon, de modifier la position des points $\alpha $ et $\beta $ à partir des nouvelles informations fournies par le premier tracé (retour à l’étape 2 de cette énumération.)
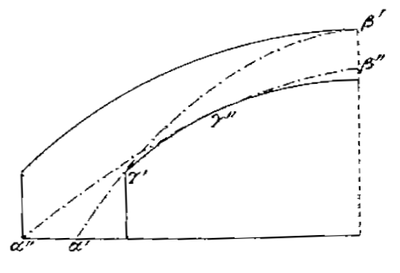
Fig 1: Lignes de pression correspondant aux poussées minimales et maximales
d’après Méry 1840 [14] – scanné par la BNF
d’après Méry 1840 [14] – scanné par la BNF
3 Modifications de l’épure de Méry au XIXe s.
Nous avons vu ci-dessus l’essentiel des indications permettant de tracer l’épure de Méry telle que son auteur l’a présenté en 1840. Nous allons maintenant exposer les différentes modifications de la méthode, mises au point dans la seconde moitié du XIXe siècle. Ces modifications vont dans le sens de la simplification et de la rapidité d’éxecution de l’épure. Afin de bien saisir les modifications par rapport à la méthode d’origine de Méry, nous commencerons cette partie par une synthèse du mémoire de 1840.3.1 Synthèse du mémoire de Méry de 1840
Exposé de la méthode Comme le titre de son mémoire l’indique, Méry s’intéresse spécifiquement aux voûtes en berceau. Il commence par définir la courbe de pression ou courbe des pressions, que nous appelons de nos jours ligne de pression (p.50). C’est la courbe formé par la suite des points d’applications des résultantes des forces (ou pressions) sur les joints. Il indique que « L’intrados et l’extrados forment deux limites dont la courbe des pressions ne doit jamais sortir, et, lorsque cela arrive, l’équilibre est impossible » (p.51). En considérant une courbe de pression, il explique que deux conditions de résistance à respecter. La première concerne la résistance en compression des de la maçonnerie. Si la courbe de pression s’approche trop prêt de l’intrados ou de l’extrados, il y a un risque d’écrasement dans ces zones. La seconde condition concerne le risque de glissement d’un voussoir sur son voisin, si l’inclinaison de la ligne de pression par rapport à la normale au joint est trop importante2. « Dans la pratique, les voûtes ont toujours une épaisseur plus forte que celle strictement nécessaire pour leur stabilité ; cette circonstance est cause que la courbe des pressions peut y prendre une infinité de positions différentes, sans qu’il soit possible de prévoir laquelle se réalisera, parce qu’elle dépend du tassement dont on ne sait pas tenir compte avec exactitude. » (p.52) Méry explique ici que la courbe de pression réelle n’est pas connue. Il indique ensuite qu’il suffit en pratique de déterminer les deux courbes de pressions correspondant aux poussées extrémales que peut exercer la voûte : celle de la poussée minimale et celle de poussée maximale. Méry indique que ces courbes de pression passent toujours par des joints particuliers dont la position peut être estimée. Il appelle ces joints joints de rupture (p.54). Il donne alors les deux méthodes de dessin que nous avons présenté ci-dessus (Cas 1 et Cas 2), qui s’appliquent aux voûtes en berceau symétriques, et qui permettent d’obtenir les lignes de pression qui sont tangentes à l’horizontale au niveau de la clé. Il est important de noter que la méthode donnée par Méry n’est pas directe. Suivant l’expérience et l’intuition du dessinateur, les points arbitraires peuvent être plus ou moins bien choisis, et c’est ensuite par tâtonnements (p.54) que se fait la recherche de la courbe de pression recherchée (de poussée minimum, ou de poussée maximum suivant les cas). C’est là tout le sens de sa phrase : « On peut donc, sans inconvénient, prendre d’abord arbitrairement les deux points nécessaires pour faire l’épure de la courbe, sauf à les rectifier ensuite. » (p.53) Application de la méthode Méry considère ensuite pour l’application de sa méthode deux situations. La première, la plus simple, est celle où la maçonnerie est considérée infiniment résistante. La seconde est celle où la maçonnerie est considérée avoir une résistance finie. Dans le premier cas, Méry indique que les courbes de pression correspondant aux pressions maximales et minimales toucheront l’intrados et l’extrados. Il montre sur un exemple comment trouver par tâtonnement la dimension minimale à donner à un arcs pour assurer leur stabilité. Dans ce cas limite, il n’existe qu’une seule ligne de pression intérieure à la maçonnerie, qui est donc a la fois la ligne de pression de poussée maximale et de poussée minimale. Méry appelle ce cas limite équilibre mathématique. Méry considère ensuite de nombreux exemples (pp.56-63 et les planches CLXXXIII et CLXXXIV), tirés des expériences de Boistard (1810 [4]), ou extraits des exemples analytiques du mémoire de Audoy (1820 [2]). Ces exemples forment le corps du mémoire (environ 40% de ce dernier), et ont probablement joué un rôle important dans le succès de la méthode, nous reviendrons sur ce point. Dans le second cas, où la résistance limitée des voussoirs est prise en compte, Méry définit de nouvelles limites plus restrictives que l’intrados et l’extrados pour assurer la stabilité (voir Fig. 2). La description de la méthode pour obtenir ces nouvelles limites est donnée succintement (pp.65-66). Pour tracer ces limites, il indique que l’intervalle compris entre la ligne de pression et le bord extérieur doit être capable de supporter les deux tiers de la résultante s’appliquant sur ce joint, et que la résistance à la compression doit être limité au dixième de sa valeur de rupture. Soulignons ici que Méry ne parle à aucun moment du tiers central de la voûte. Il ne donne pas d’exemple concret d’application où la résistance finie de la maçonnerie est prise en compte (en dehors de la figure 2).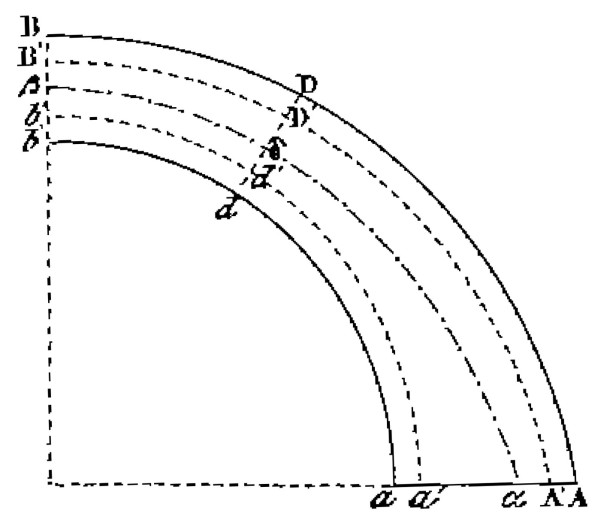
Fig 2: Réduction du domaine admissible pour les lignes de pression
d’après Méry 1840 [14] – scanné par la BNF
d’après Méry 1840 [14] – scanné par la BNF
3.2 Introduction aux modifications du XIXe s.
Les modifications apportées à la méthode de Méry concernent le choix des points $\alpha $ et $\beta $ pour tracer la ligne de pression, et plus généralement la position de cette ligne de pression à l’intérieur de la maçonnerie. Pour choisir les points de départs de l’épure, deux choix successifs sont réalisés. Le premier choix est celui des joints de rupture. Par exemple dans le cas de la ligne de pression de poussée minimum, faut-il placer le point $\alpha $ sur le joint situé à 30, 35, 40 o etc. par rapport à l’horizontale ? Une fois choisi le joint de rupture, le second choix consiste à positionner la résultante des forces (ou pressions) sur le joint choisi : sur l’extrados, sur l’intrados, ou plus à l’intérieur du joint ? Ces deux choix sont naturellement liés, mais il est nécessaire de les distinguer pour bien comprendre l’évolution que va connaître l’épure de Méry au XIXe siècle.3.3 Choix des joints de rupture
Le choix de la position des joints de rupture n’est pas donné par Méry, même si ce dernier indique qu’on peut facilement se donner une idée de leur position. La méthode de Méry, qui s’applique à des demi-voûtes symétriques, nécessite de trouver deux joints de rupture pour permettre le dessin de la ligne de pression. Pour le dessin de la poussée minimale, le premier joint de rupture est généralement placé à la clé. Bien qu’il existe des cas particuliers, comme les arcs brisés (ogives) où la clé n’est pas un joint de rupture, ce que fait remarquer Méry dans son mémoire, cette hypothèse est généralement assez bonne, et en tout cas n’est pas remise en cause par les auteurs qui reprennent la méthode de Méry au XIXe siècle. En revanche, le choix de la position du joint de rupture sur l’intrados pour la détermination de la poussée minimum fait l’objet de différentes approches, que nous présentons maintenant. Approche par tâtonnements L’approche par tâtonnement pour trouver les joints de rupture est celle de la méthode d’origine, proposée par Méry lui-même. Il choisit deux joints de rupture arbitraires, au sens où il utilise l’intuition pour choisir ces positions, mais rien ne garantit que ce choix soit exact. Si la position du joint de rupture choisie n’est pas exacte, alors la ligne de pression trouvée sort du domaine admissible. Cette information est alors utilisée pour corriger la position du joint de rupture. Méry qualifie lui-même cette démarche de tâtonnements. Approche forfaitaire du joint de rupture L’approche forfaitaire simplifie l’application de la méthode de Méry. Elle consiste à prendre des valeurs forfaitaires pour l’angle qui définit la position du joint de rupture inférieur. Nous reproduisons ci-dessous les valeurs forfaitaires proposées par Croizette-Desnoyers. La position des joints de rupture est choisie une fois, et n’est pas modifiée par la suite.Approche géométrique du joint de rupture Il est possible d’estimer la position du joint de rupture inférieur à l’aide d’un petit dessin géométrique. Le joint de rupture est l’unique joint dont la tangente à l’intrados (ou au tiers-central inférieur) passe par le point K, point d’intersection entre l’horizontale définie par la poussée à la clé, et la verticale passant par le centre de gravité de la portion de voûte entre le joint étudié et la clé (Fig. 4). Pillet trace sur cette figure3 successivement les points K, K’ et K », qui correspondent aux joints AB AB’et AB », pour illustrer graphiquement cette propriété (1895 [17]).La valeur de la poussée P ne peut être connue exactement que lorsqu’on a déterminé le joint pour lequel $bq/y$ [nota : traduction mathématique de la méthode de Méry] ; mais pour les voûtes de dimensions ordianaires, cette position varie peu et on admet généralement que les angles formés avec l’horizontale, par le prolongement de ce joint, ont les valeurs ci-après :[…] On peut donc sans inconvénient, lorsqu’il s’agit seulement de calculs approximatifs, prendre pour base les valeurs d’angles signalées plus haut. Croizette-Desnoyers 1885 [9,p.412]
- Pour le plein cintre 30o
- Pour l’ellipse surbaissée à 1/3 45o
- Pour l’ellipse surbaissée à 1/4 50o
- Pour l’arc de cercle surbaissé à 1/5 47o
- Pour l’arc de cercle surbaissé au delà de 1/5 > 47o
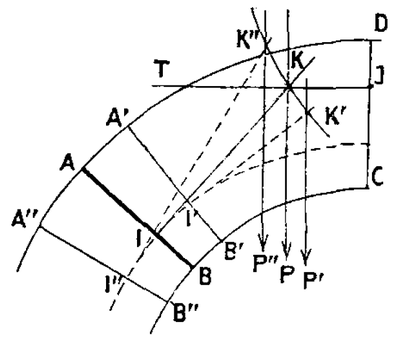
Fig 4: Détermination géométrique du joint de rupture
d’après Pillet 1895 [17,p.430 fig.452] – scanné par l’Ecole Centrale de Lyon
d’après Pillet 1895 [17,p.430 fig.452] – scanné par l’Ecole Centrale de Lyon
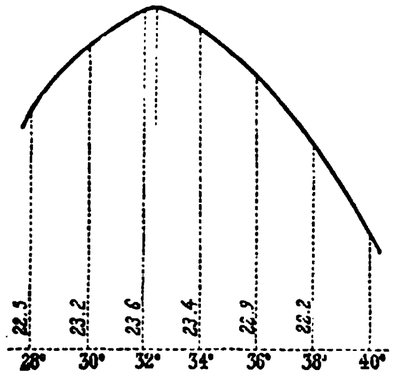
Fig 5: Détermination du joint de rupture
d’après Croizette-Desnoyers 1885 [9,p.431] – scanné par Google
d’après Croizette-Desnoyers 1885 [9,p.431] – scanné par Google
3.4 Apparition du tiers-central
Tant que la résistance de la maçonnerie à la compression est considérée infinie, la méthode graphique de Méry est simple et élégante par rapport aux méthodes analytiques proposées par les autres auteurs avant lui. Cependant, les choses se compliquent pour tenir compte de la résistance finie de la maçonnerie. La méthode que propose Méry consiste à réduire le domaine admissible pour la ligne de pression, c’est à dire la zone où la ligne de pression peut se trouver sans risquer l’écrasement de la maçonnerie. Cette réduction du domaine de stabilité, qui apparait sur la Fig. 2 ci-dessus, est un processus qui nécessite des calculs (ce n’est pas un simple tracé géométrique), qui n’est de plus que très succinctement décrit dans son mémoire5. Contrairement au cas où la résistance à la compression est infinie où Méry donne de nombreux exemples d’application, aucun exemple n’est fourni pour le cas avec résistance finie. L’utilisation du tiers-central permet de remplacer les calculs proposés à l’origine par Méry pour modifier le domaine admissible de la ligne de pression par une simple opération géométrique. Le domaine admissible pour la ligne de pression est simplement réduit au tiers-central de la maçonnerie. L’utilisation du tiers-central apparait sur les figures 4 et 6.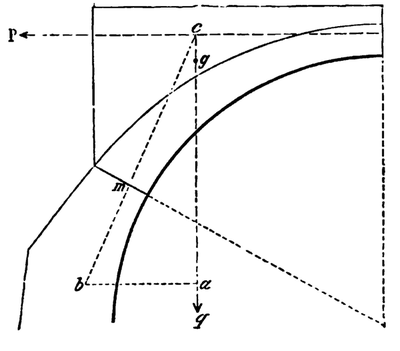
Fig 6: Détermination de la poussée, avec utilisation du tiers central
d’après Croizette-Desnoyers 1885 [9,p.431] – scanné par Google
d’après Croizette-Desnoyers 1885 [9,p.431] – scanné par Google
4 Approche historique de l’épure de Méry
Après avoir exposé dans les parties précédentes l’épure de Méry dans sa forme d’origine puis les modifications qui y ont été apportées, nous allons chercher à présent à retracer cette évolution d’un point de vue historique.4.1 Apparition de la règle du tiers-central
La méthode proposée par Méry pour tenir compte de la résistance de la maçonnerie ne semble pas avoir connu le même succès que le reste du mémoire. Le seul traité que nous ayons trouvé reproduisant cette partie de la méthode de Méry est le traité de Construction de Breymann 1849 [5,p.208], qui propose une traduction assez proche du texte du mémoire d’origine, avec la suppression de quelques passages (exemples d’application, partie théorique finale). Les traités de construction ne font généralement pas référence à la réduction du domaine admissible pour la ligne de pression tel qu’elle fut proposé par Méry (e.g. Claudel et Laroque 1850 [7,pp.324-327]). L’approche élastique, présentée notamment par Navier dans son cours (1839 [15]), conduit à la règle du tiers-central. Comme le note Delbecq, Navier déduit du comportement élastique du matériau la règle du tiers central, à savoir que le centre de pression sur un joint doit se trouver à l’intérieur du tiers central […] (1983 [10,p.73]). Cette règle du tiers-central, qui ne figure initialement pas dans l’épure de Méry de 1840, permet de simplifier grandement la réduction du domaine admissible pour la ligne de pression. Elle va être progressivement adoptée par l’ensemble des auteurs qui présentent la méthode de Méry. Nous avons trouvé un premier exemple de l’utilisation du tiers central avec la méthode de Méry chez Fontaine en 1865. Il écrit un article sur la stabilité des voûtains en briques des planchers en fer, dans les Nouvelles annales de la construction, publiées par Oppermann [13]. L’utilisation du tiers-central devient par la suite systématique dans les traités de construction qui présentent l’épure de Méry et que nous avons pu consulter : Croizette-Desnoyers 1885 [9,p.427], Résal 1887 [18], Pillet 1895 [17], Barré 1896 [3] etc.4.2 Choix des joints de rupture
L’épure de Méry se déroule en deux phases. La première, très rapide, permet de déterminer la poussée de la voûte pour la ligne de pression en cours de dessin, dont on ne connaît pas encore la forme complète. La seconde, est le dessin de cette ligne de pression, pour vérifier que les hypothèses de départ sont correctes. La poussée d’une ligne de pression est connue avant même que la ligne de pression ne soit tracée. Si une erreur apparaît, par exemple si la ligne de pression travée sort des limites de la maçonnerie, on peut alors modifier ces hypothèses et recommencer le procédé. Nous avons vu ces différentes étapes dans la première partie de cet article. Les différentes modifications proposés dans les traités de construction du XIXe siècle vont dans le sens d’une simplication importante de la méthode. Des méthodes rapides sont données pour choisir la position du joint de rupture, qui n’est ensuite plus modifié. L’approche forfaitaire du joint de rupture est proposée par Croizette-Desnoyers 1885 [9]. Résal et Pillet proposent en 1887 et 1895 l’approche géométrique de détermination du joint de rupture inférieur. Ce choix unique du joint de rupture permet de négliger de tracer la ligne de pression elle-même, car si le joint de rupture est correctement choisi, la ligne de pression est nécessairement à l’intérieur de la maçonnerie. L’épure de Méry ainsi réalisée ne permet pas de vérifier la stabilité de la voûte elle-même, mais seulement de trouver très rapidement la poussée de la voûte, qui servira à s’assurer de la stabilité de ses appuis. A contrario, il faut noter que Méry représente toujours sur les figures de son mémoire la ligne de pression dessinée en intégralité. Certains auteurs relèvent que cette simplification extrême de l’épure de Méry n’est pas applicable dans toutes les situations. Ainsi Croizette-Desnoyers souligne que son approche forfaitaire est une approximation qui peut être utilisée dans certains cas. Il ne recommande pas l’utilisation systématique de l’approche forfaitaire pour trouver le joint de rupture.4.3 Succès du mémoire
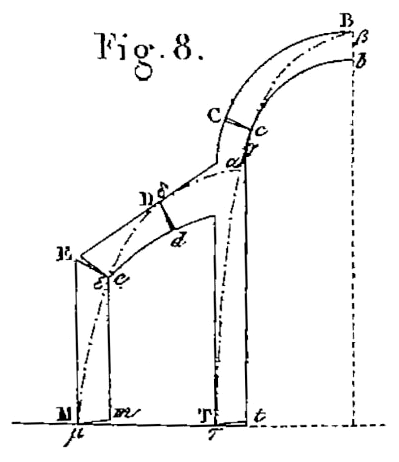
Le mémoire de Méry connaît un succès immédiat. Une médaille d’or distinguant le meilleur mémoire publié en 1840 dans les annales des Ponts et Chaussées est accordée à Méry en 1842 (1842 2sem p.129). Dans les années qui suivent, de nombreux mémoires des annales des Ponts et Chaussées font référence au mémoire de Méry, généralement sous des termes élogieux (1844, 1851, 1853, 1855, 1856, 1860, 1865). Dupuit6 en 1870 [11], Résal7 en 1887[18], et Abraham8 en 1934[1] soulignent la popularité de la méthode de Méry dans la pratique des ingénieurs. La méthode de Méry est d’ailleurs présentée dans la grande majorité des traité de construction, sous sa forme d’origine (Claudel et Laroque 1850), ou sous des formes modifiées (Croizette-Desnoyers 1885, Résal 1887). On trouve également la méthode de Méry dans un traité de construction allemand, qui est également traduit et publié en Italie (Breymann 1849 [5,pp.205-209]). Breymann semble cependant un peu réservé quant-à l’utilisation pratique de la méthode de Méry9. Comment expliquer un tel succès de l’épure de Méry ? Il y a, en premier lieu, le côté novateur. Méry est le premier en France à définir et exploiter le concept de courbe de pression. Moseley fait de même en Angleterre à peu près la même époque. Cette méthode a de plus un caractère géométrique fort, et donc facilement communicable qui ajoute à son attrait. Il suffit pour cela de la comparer aux équations analytiques de Navier (1839 [15]), ou aux longs tableaux numériques de Petit (1835[16]) qui tente de simplifier l’utilisation des approches analytiques. Enfin, Méry donne dans son mémoire de nombreux cas d’applications qui s’appuient notamment sur les expériences réalisées par Boistard. Il illustre ainsi de manière convaincante les possibilités de la méthode qu’il propose. Tous les exemples traités par Méry dans son mémoire figurent la courbe de pression complète, ce qui suppose un certain nombre de constructions graphiques intermédiaires. Ces dessins intermédiaires ne sont pas tracées sur les planches du mémoire qui ne présentent que les résultats finaux. Malgré son apparante simplicité, la méthode de Méry de 1840 est donc relativement longue à dessiner. Une autre raison du succès de l’épure de Méry, est liée aux modifications apportés au XIXe à la méthode, qui rendent son application plus simple et plus rapide. La méthode de Méry modifiée est moins précise dans son résultat mais beaucoup plus rapide si l’objectif est seulement de trouver la poussée minimale d’une voûte. Nous donnons sur la Fig. 7 les tracés géométriques nécessaires avec la méthode de Méry modifiée à gauche, et à droite celle utilisant le tracé du funiculaire complet. On voit à quel point l’épure de Méry est plus rapide pour obtenir la valeur de la poussée. Cette rapidité ce fait donc au détriment de la connaissance de la courbe des pressions. Ici, les points de passage de la courbe des pressions font partie des pré-supposés de l’étude.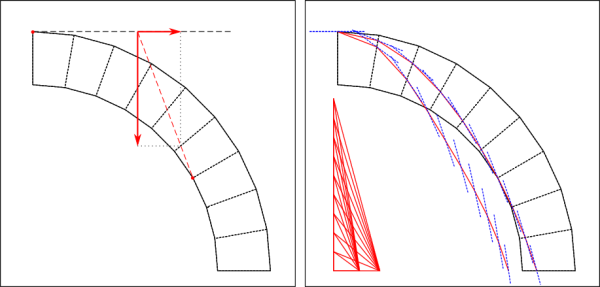
Fig 7: Détermination de la poussée minimum d’un arc
Epure de Méry à gauche, méthode du funiculaire à droite
Epure de Méry à gauche, méthode du funiculaire à droite
4.4 Redécouverte du mémoire de 1840
En dehors de ce mémoire qui le rendra célèbre, Méry ne semble pas avoir publié d’autres mémoires ou ouvrages sur la stabilité des voûtes. Sa méthode est donc connue principalement par les traités de construction, qui eurent tous ensemble une diffusion évidemment plus large que le mémoire d’origine inclut uniquement dans le premier volume des annales des Ponts et Chaussées de 1840. Etant donné que la méthode est progressivement modifiée au XIXe siècle dans ces différents traités, il n’est pas étonnant qu’une certaine confusion règne sur l’épure de Méry. Colette attribue ainsi à Méry des hypothèses qui sont en réalité postérieures à son mémoire (tiers-central, joint de rupture fixé à 30o (Colette 1982 [8,p.83]). Il semble que l’on doive à Delbecq la redécouverte de la juste valeur du mémoire de Méry de 1840 (Delbecq 1983 [10,pp.73-75,78-85]), qui a depuis été soulignée à plusieurs reprises (e.g. Foce et Aita 2003 [12]).4.5 Conclusion
Le succès de la méthode de Méry au XIXe siècle, et la poursuite de son enseignement au XXe siècle est probablement due à sa simplicité d’utilisation. Elle permet, au moyen d’un nombre réduit de dessins géométriques, de définir un état d’équilibre possible pour la voûte. L’application de la méthode de Méry sous sa forme de 1840, avec la prise en compte de la résistance limitée de la maçonnerie, n’a pas connu le succès de la version simplifiée de l’épure de Méry, en raison de sa difficulté de mise en œuvre. L’apparition des calculs sur ordinateur a permis de remplacer les dessins manuels par des calculs numériques, en réduisant ainsi à la fois le temps d’éxecution, et les risques d’erreur et d’imprécisions des dessins. La méthode de Méry sous sa forme la plus complexe est aujourd’hui applicable en quelques clics.Article mis en ligne le : 07/01/2015.
Révisé le : 08/01/2015.
Sur l’auteur :
Mathias Fantin est ingénieur structure et docteur en architecture, et il travaille sur la restauration des monuments anciens. Il a fondé en 2014 Bestrema, un bureau d’études structures spécialisé dans ce domaine. Ces autres articles pourraient également vous intéresser :- Décintrement des voûtes -
 Le décintrement est une étape critique de la construction des voûtes. Il dépend du type de voûte construit (pont, édifice), des matériaux (pierres et mortiers) et aura une incidence sur le chargement, les tassements et les fissures.
Le décintrement est une étape critique de la construction des voûtes. Il dépend du type de voûte construit (pont, édifice), des matériaux (pierres et mortiers) et aura une incidence sur le chargement, les tassements et les fissures. - Résistance et stabilité des remplages -
 Vérification de la résistance et stabilité des remplages, supports en pierre des vitraux dans les édifices gothiques.
Vérification de la résistance et stabilité des remplages, supports en pierre des vitraux dans les édifices gothiques. - La géométrie des voûtes -
 La géométrie des voûtes renvoie à deux concepts : la forme de l’intrados et l’appareil. Étude des correspondances et divergences entre les deux.
La géométrie des voûtes renvoie à deux concepts : la forme de l’intrados et l’appareil. Étude des correspondances et divergences entre les deux.
Bibliographie
- [1]
- P. ABRAHAM : Viollet-le-Duc et le rationalisme médiéval. Vincent, Fréal et Cie, Paris, 1934. BPI.
- [2]
- AUDOY : Mémoires sur la poussée des voûtes en berceau. In Memorial de l’officier du Génie, num. 4. 1820.
http://books.google.fr/books?id=KqA8AAAAYAAJ - [3]
- P. BARRé et L. BARRé : Memento de l’architecte et de l’entrepreneur. Théorie pratique et législation du bâtiment. E. Bernard, Paris, 1896.
http://gallica.bnf.fr/ark:/12148/bpt6k58247805 - [4]
- L.-C. BOISTARD : Expériences sur la stabilité des voûtes. In Recueil de divers mémoires extraits de la Bibliothèque impériale des ponts et chaussées de P.-C. Lesage, vol. 2, p. 171-217. Firmin Didot, Paris, 1810.
books.google.fr/books?id=BIMOAAAAYAAJ - [5]
- G. A. BREYMANN : Bauconstructionslehre Vol 1 Constructionen in Stein. Hoffmann’sche Verlags-Buchhandlung, Stuttgart, 1849.
http://www.e-rara.ch/zut/content/titleinfo/8642550 - [6]
- J. CLAUDEL : Formules, tables et renseignements usuels ; aide-mémoire des ingénieurs, des architectes, etc. Victor Dalmont, Paris, 6e édn, 1864.
http://www.google.fr/books?id=VF5AAAAAcAAJ - [7]
- J. CLAUDEL et L. LAROQUE : Pratique de l’art de construire – Maçonnerie. Carilian-Goeury et V. Dalmont, Paris, 1850.
http://www.google.fr/books?id=zygOb89Ro1MC - [8]
- B. COLETTE : Viollet-le-Duc et la pensée mathématique au XIXe siècle. In Actes Du Colloque International Viollet-Le-Duc, Paris, 1980, Paris, 1982. Nouvelles Editions Latines.
http://books.google.fr/books?id=jl7i0uF4pVgC - [9]
- P. CROIZETTE-DESNOYERS : Cours de construction des ponts, vol. 1. Dunod, Paris, 1885.
http://books.google.fr/books?id=9fc4AAAAMAAJ - [10]
- J. DELBECQ : Analyse de la stabilité des ponts en maçonnerie par la théorie du calcul à la rupture. Thèse de doctorat, Ecole nationale des ponts et chaussées, Paris, 1983.
- [11]
- J. DUPUIT : Traité de l’équilibre des voutes et de la construction des ponts en maçonnerie. Dunod, Paris, 1870.
- [12]
- F. FOCE et D. AITA : The Masonry Arch Between « Limit » and Ëlastic » Analysis. A critical re-examination of Durand-Claye method. In Proceedings Of The First International Congress On Construction History, Madrid, 20th, vol. 2, p. 895-908, 2003.
- [13]
- H. FONTAINE : Expériences faites sur la stabilité des voûtes en brique. Nouvelles annales de la construction, nov. 1865.
http://gallica.bnf.fr/ark:/12148/cb32826369p/date - [14]
- E. MéRY : Equilibre des voûtes en berceau. Annales des ponts et chaussées, p. 51-70, 1840.
http://gallica.bnf.fr/ark:/12148/cb34348188q/date - [15]
- C.-L. NAVIER : Résumé des leçons données à l’école des ponts et chaussées, sur l’application de la mécanique à l’établissement des constructions. Hauman et Compagnie, Bruxelles, 1839.
http://www.google.fr/books?id=iVQJAAAAIAAJ - [16]
- PETIT : Mémoire sur le calcul des voûtes circulaires. In Mémorial de l’officier du génie, num. 12, p. 73-150. de Fain, Paris, 1835.
http://www.google.fr/books?id=zX8OAAAAYAAJ - [17]
- J. PILLET : Traité de stabilité des constructions. Librairie polytechnique de Baudry et compagnie, Paris, 1895.
- [18]
- J. RéSAL : Ponts en maçonnerie – Tome 1 – Stabilité des voûtes, vol. 1 de Encyclopédie des travaux publics – Ponts en maçonnerie. Baudry, Paris, 1887.
http://gallica.bnf.fr/ark:/12148/bpt6k91083k
Notes
1 « Dans son Mémoire historique, M. Poncelet dit que c’est à tort qu’on attribue l’initiative des recherches sur les propriétés de la courbe des pressions à M. Méry, qui ne s’en serait occupé que quelques années après M. Moseley. Dans sa traduction de la Théorie des voûtes de Scheffler, M. Victor Fournié établit les titres de priorité de M. Méry. Son travail est resté manuscrit jusqu’en 1840, mais il avait été fait en 1827; celui de M. Moseley n’a été publié qu’en 1833 dans le Philosophical Magazine. » Dupuit 1870 [11,p.118]
2 « La courbe des pressions donne la mesure de cette tendance au glissement, par l’inclinaison sur chaque joint. » Méry montre que ce n’est qu’une approximation, valable si la résultante est tangente à la courbe des pression, « ce qui n’est rigoureusement vrai qu’aux endroits où celle-ci passe par le centre de gravité d’un voussoir. » p.52
3 Nous avons simplifié la figure par rapport à la figure d’origine, pour ne garder que les dessins qui concernent la détermination du joint de rupture.
4 Méry note et démontre que la résultante des forces n’est tangente à la ligne de pression que si la ligne de pression est proche du centre de gravité des blocs
5
Nous avons déjà développé l’analogie que l’on peut trouver entre cette méthode avec considération de la résistance et les résultats du calcul à la rupture présentés par Delbecq (voir notre précédent article, les coefficients de sécurité des voûtes).
6
« Nous insistons d’autant plus sur ce qui nous paraît défectueux et inexact dans le mémoire de M. Méry, que le procédé géométrique dont il a enrichi la science l’a rendu très populaire et qu’il a passé dans la pratique générale des ingénieurs et des architectes. Nous en avons nous-même largement usé dans le chapitre précédent ; nous serions donc désolé qu’on vît dans la critique que nous en faisons l’intention d’en diminuer la valeur. » Dupuit 1870 [11,p.121]
7
« La méthode de M. Durand-Claye […] ne semble pas avoir pénétré dans la pratique. Nous en trouvons la raison […] dans la complication et le nombre des constructions graphiques qu’entraîne cette méthode. C’est là évidemment ce qui a rebuté les constructeurs habitués à la règle de M. Méry, dont l’emploi, s’il ne donne pas des renseignements concluants, n’exige que des constructions simples et rapides. » Résal 1887 [18,p.99]
« La règle pour le tracé des courbes des pressions, que nous venons d’exposer [celle de Méry], est restée, quoique la plus ancienne en date, la plus usitée, par suite de sa commodité et de sa simplicité ; elle a en somme reçu la consécration de l’expérience et donne toujours des indications utiles au constructeur. » Résal 1887 [18,p.85] 8 « Ce mode de déformation des arcs plein cintre se divisant en quatre voussoirs se comportant comme s’ils étaient articulés a permis de concevoir le moyen empirique d’évaluer leur poussée connu sous le nom de méthode de Méry (5). Elle est si simple et si satisfaisante qu’elle est encore employée aujourd’hui, concurremment avec les méthodes plus précises, basées sur les déformations élastiques (6), pour l’étude des ponts en maçonnerie. » Pol Abraham 1934 [1,p.10] 9 « Poi questa applicazione, quantunque non contenga difficoltà di sorta, richiede tempo e fatica, perché le giuste dimensioni della vôlta si possono trovare solo mediante parecchi tentativi, ed ogni variazione di dimensioni che si imprende a considerare richiede una determinazione dei baricentri, che riesce piuttosto laboriosa » – La traduction italienne de la cinquième édition de 1885 de Breymann (elle même refaite par H. Lang de Karlshuhe) contient les mêmes informations, et ne semble pas apporter de changement au jugement de la première édition de Breymann.
« La règle pour le tracé des courbes des pressions, que nous venons d’exposer [celle de Méry], est restée, quoique la plus ancienne en date, la plus usitée, par suite de sa commodité et de sa simplicité ; elle a en somme reçu la consécration de l’expérience et donne toujours des indications utiles au constructeur. » Résal 1887 [18,p.85] 8 « Ce mode de déformation des arcs plein cintre se divisant en quatre voussoirs se comportant comme s’ils étaient articulés a permis de concevoir le moyen empirique d’évaluer leur poussée connu sous le nom de méthode de Méry (5). Elle est si simple et si satisfaisante qu’elle est encore employée aujourd’hui, concurremment avec les méthodes plus précises, basées sur les déformations élastiques (6), pour l’étude des ponts en maçonnerie. » Pol Abraham 1934 [1,p.10] 9 « Poi questa applicazione, quantunque non contenga difficoltà di sorta, richiede tempo e fatica, perché le giuste dimensioni della vôlta si possono trovare solo mediante parecchi tentativi, ed ogni variazione di dimensioni che si imprende a considerare richiede una determinazione dei baricentri, che riesce piuttosto laboriosa » – La traduction italienne de la cinquième édition de 1885 de Breymann (elle même refaite par H. Lang de Karlshuhe) contient les mêmes informations, et ne semble pas apporter de changement au jugement de la première édition de Breymann.