Résistance et stabilité des remplages

1 Introduction

Les remplages, supports des vitraux dans les édifices religieux, sont un élément aussi caractéristique de l’architecture gothique que le sont les voûtes. L’évaluation de leur résistance et de leur stabilité a cependant fait couler beaucoup moins d’encre que celle des voûtes. Exposés aux tempêtes, les remplages ont été progressivement amincis au cours de l’histoire dans la quête d’une plus grande légèreté visuelle et d’une plus grande transparence à la lumière. Et ce jusqu’à atteindre la limite de leur résistance, ce dont témoigne certains effondrements ou reconstructions de remplages particulièrement ambitieux, comme celui de la grande baie sud du bras sud du transept de la cathédrale de Nantes (reconstruit vers 1641 quelques années après sa construction) ou les fenêtres hautes du transept de la cathédrale de Bayeux (remplages remplacés au début du XIX^e siècle par un treillage métallique, jusqu’à leur progressive restauration depuis 2019).

Fig 1: Exemples de remplages, cathédrale de Bayeux, de Chartres et d’Orléans

La stabilité des remplages dépend à la fois de la résistance des pierres qui composent le remplage et, dans une moindre mesure en général, des barres métalliques, appelées barlotières, qui portent les panneaux de vitrail.

Lors de la construction des remplages au Moyen Âge, ces derniers ne faisaient pas l’objet d’un dimensionnement par le calcul au sens où on l’entend aujourd’hui. Il existait probablement des règles de proportion, comme pour la conception des arcs et des voûtes (Huerta Fernández, 2006), mais ces dernières ne sont pas connues pour les remplages¹. Un ensemble de vérifications (résistance à la compression, au flambement, à la pression du vent etc.) a été proposé par Ungewitter à la fin du XIX^e siècle dans son ouvrage sur les constructions gothiques (Ungewitter et Mohrmann, 1903). Ungewitter prend soin, à plusieurs reprises, d’insister sur la bonne concordance de ses résultats avec l’expérience que nous livrent les édifices gothiques.

Nous présentons dans cet article un résumé de ces vérifications, complétés par nos observations. On retiendra, comme souvent pour les monuments anciens, le caractère anachronique de ces vérifications calculatoires. Néanmoins, elles permettent de poser un cadre explicite pour comparer les remplages entre-eux du point de vue de leur résistance et stabilité.

Rappelons en introduction quelques éléments de vocabulaire qui seront utilisés dans la suite. On note en italique les termes en anglais et allemand pour faciliter la lecture de Ungewitter et Mohrmann (1903).

remplage : ensemble des assises et claveaux en pierre de taille qui divisent l’ouverture en plusieurs compartiments (lancettes, roses, écoinçons etc.) – tracery, Masswerk
meneau : « élément vertical d’un remplage » (Pérouse de Montclos, 2007, p.195 ) – mullion, Pfosten
demi-meneau, meneau de rive : demi-meneau construit contre le jambage – half-mullion, wall mullion, Wandpfosten
réseau : partie du remplage situé au-dessus des meneaux
barlotières : barres métalliques horizontales, supports du vitrail – storm bars, Sturmstangen. Le vitrail est fixé sur les barlotières par le moyen d’un feuillard (cover bar, Deckschiene) fixé par des clavettes traversant des pannetons placés tous les 20 à 30cm (projecting clamps, Lappen, Krampen)
vergettes : barres métalliques de faible section (6 à 10mm selon Ungewitter) qui permettent de renforcer les panneaux de vitrail contre les efforts horizontaux du vent

2 Les meneaux

2.1 Section des meneaux

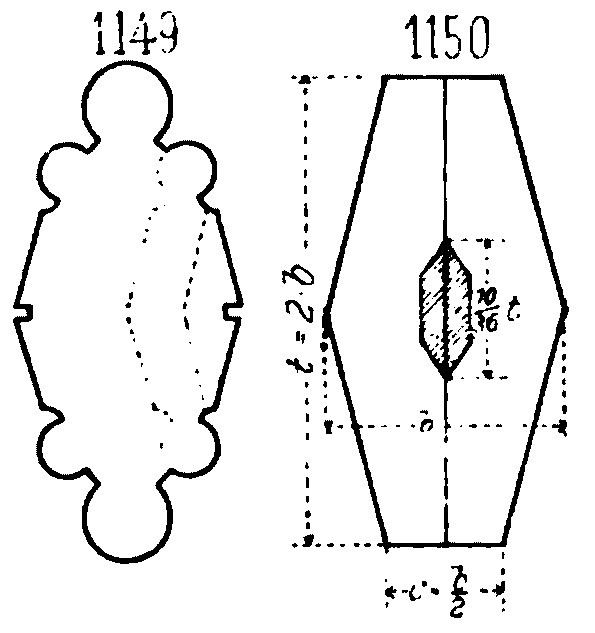
Les meneaux forment des supports verticaux très élancés. Leur section présente une dimension perpendiculaire à la baie supérieure à la dimension dans le plan de la baie. Cette disposition est presque systématique, car elle permet de laisser passer le plus possible la lumière (Ungewitter et Mohrmann, 1920, p.677). De plus, le meneau est ainsi placé dans sa position la plus favorable pour résister à la pression du vent.

Pour simplifier ses calculs, Ungewitter considère une section type (Fig. 2). Après simplification de la mouluration, la section du meneau présente un rapport profondeur $t$ sur largeur $b$ égal à 2, avec une aire $A=1,5b^2$ et des moments quadratiques $I_y=\frac{5}{12}b^4$ et $I_z=\frac{5}{64}b^4$ (Ungewitter et Mohrmann, 1920, p.677).

Fig 2: Section type d’un meneau, d’après Ungewitter et Mohrmann (1903, Tafel CXIV)

2.2 Détails constructifs

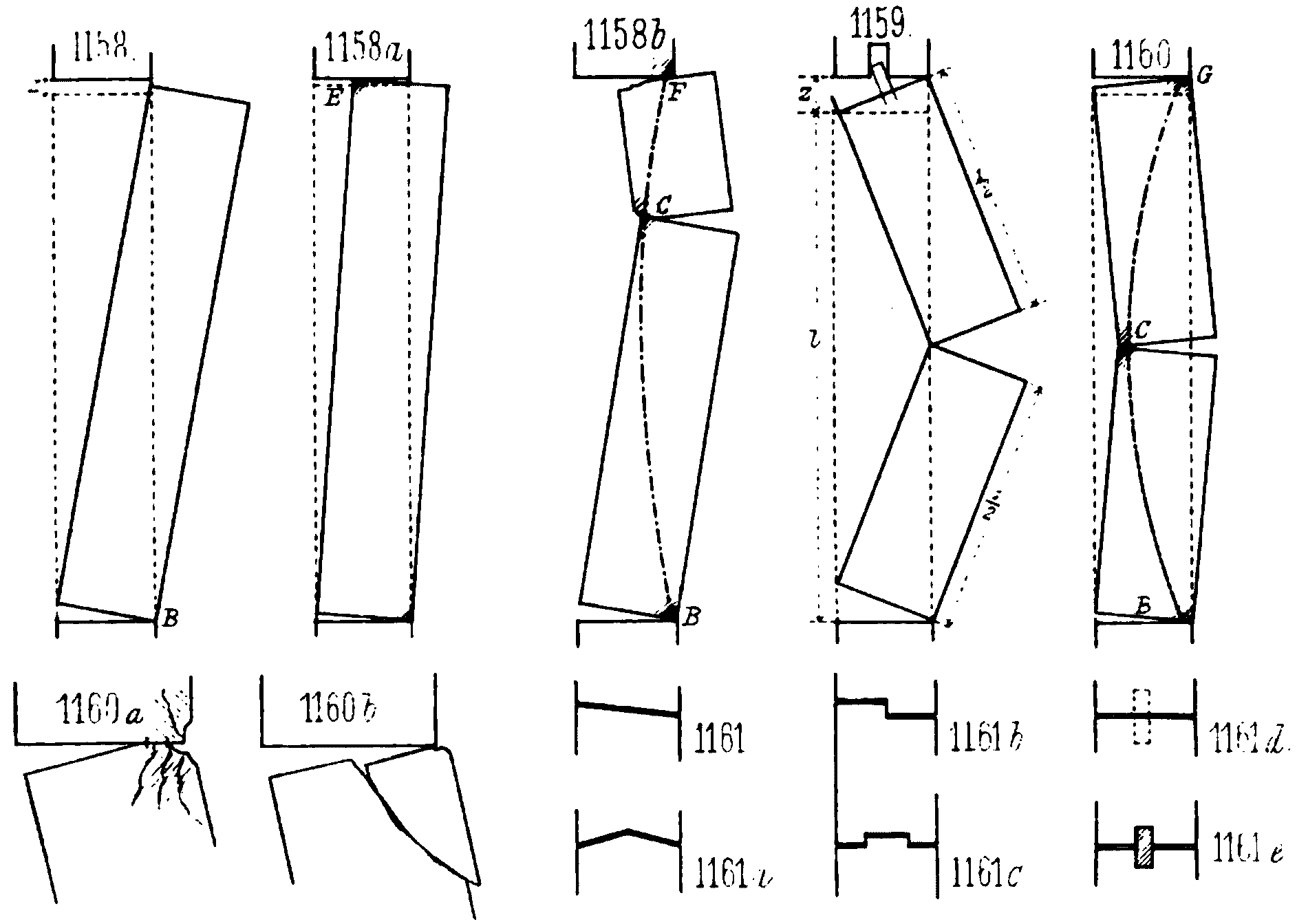
Le montage du remplage pouvait avoir lieu avant ou après la fermeture de l’arc couvrant la baie (Ungewitter et Mohrmann, 1920, p.677,685). Les deux méthodes présentent des avantages et des inconvénients. Dans le premier cas, il y a un risque d’écrasement du remplage, et de petites cales en plomb pouvaient être mis en place entre le remplage et l’arc de la baie pour éviter un transfert de charges trop importants lors de la construction des maçonneries à l’aplomb de la baie (p.685). Dans le même temps la mise en compression du remplage joue un rôle favorable dans la résistance et la rigidité sous la poussée horizontale du vent. Dans le second cas, il y a moins de risque d’écrasement du remplage, mais il peut se former un joint vide entre le réseau et l’arc de la baie. Ce vide, même s’il est limité à 0,5 ou 1,0mm peut donner lieu à des mouvements et des pressions sur les arêtes des claveaux pouvant créer des épaufrures (p.685).

Ungewitter recommande lorsque les joints sont au mortier de ciment d’insérer au moins un joint en plomb en tête ou en pied (voir 3 joints, en tête en pied et au milieu) (Ungewitter et Mohrmann, 1920, p.686).

Ungewitter présente également la conséquence de l’apparition de fissures dans les joints des meneaux, en particulier avec le risque de glissement du joint. Il décrit les divers procédés pour éviter le glissement (goujons, crossettes, tenons etc., voir 1158 à 1161 sur figure 3). Il met en lumière un risque de glissement d’autant plus fort que les pierres qui composent les meneaux sont élancées (rapport $L_m/t$, p.687-8).

Fig 3: -, d’après Ungewitter et Mohrmann (1903, Tafel CXIV)

Le remplage est bloqué dans le cadre de la baie par la coupe des pierres à la liaison avec l’arc et le piédroit de la baie (Fig. 4). (Ungewitter et Mohrmann, 1920, p.677).

Fig 4: Insertion du réseau dans la baie, d’après Ungewitter et Mohrmann (1903, Tafel CXIII)

UNGEWITTER ET MOHRMANN (1920, P.686)
The best solution always remains one sufficiently heavy, with simple or compound tracery, that does not require the aid of the window arch at all, or only needs to stress it in the urgent cases. The magnitude of the load of the masonry built above the window is then made entirely independant of the window itself.

2.3 Vérifications de la résistance et stabilité

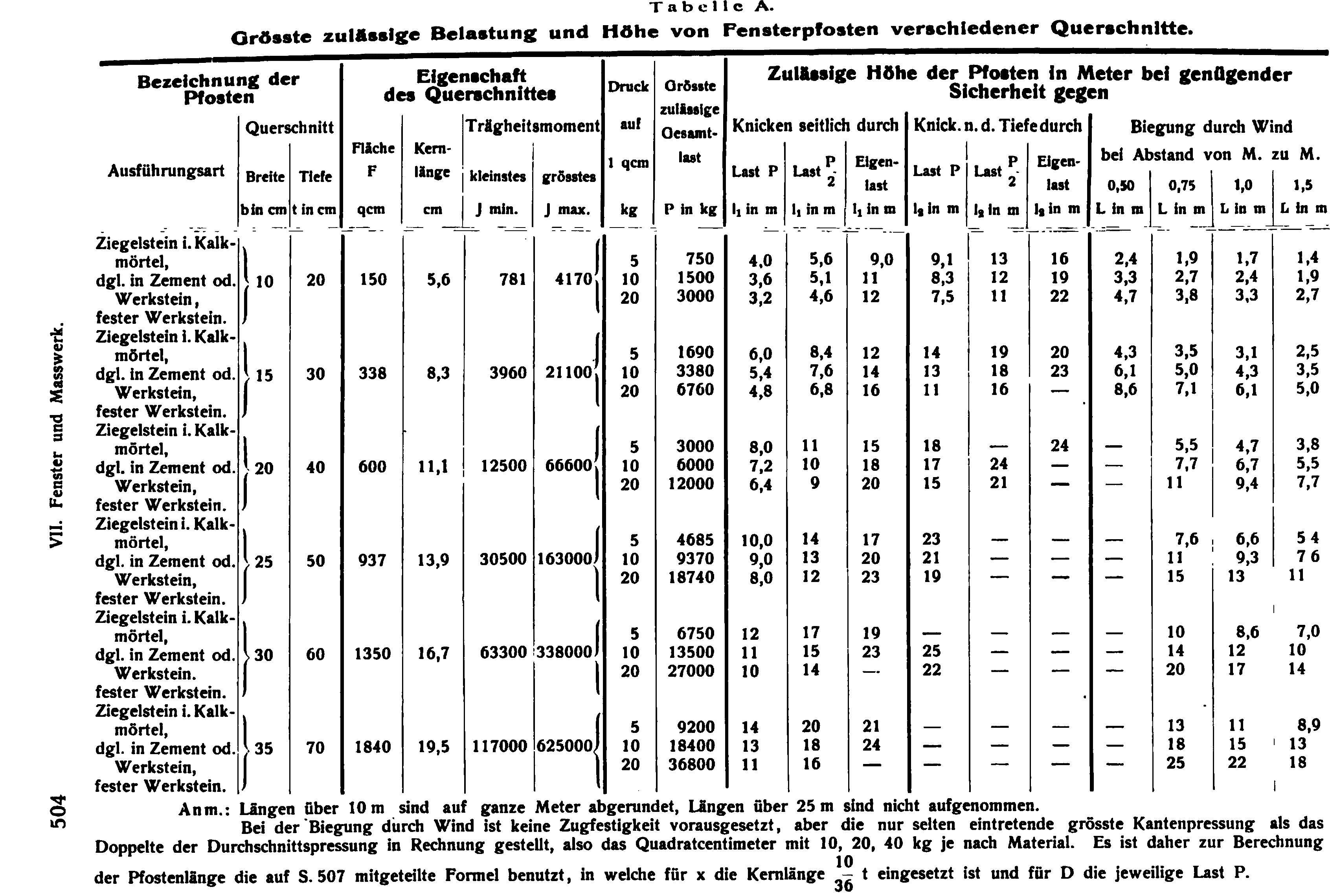
Pour vérifier le dimensionnement d’un meneau avec la section type présentée précédemment, Ungewitter considère successivement la résistance de la pierre sous compression centrée, la stabilité face au risque de flambement et enfin la résistance sous l’effet du vent.

Compression centrée Pour la résistance des meneaux à la compression (centrée), Ungewitter donne le chargement maximum $P$ pour trois types de maçonneries : maçonnerie de brique avec mortier de chaux (0,5MPa), maçonnerie de « bonnes » briques avec mortier de ciment ou pierre de taille ordinaire (1,0MPa), et pierre de taille en pierre dure posée avec un soin particulier (2,0MPa). Ces contraintes s’entendent comme des contraintes admissibles intégrant un coefficient de sécurité de 10 (cela est précisé par Ungewitter).

Flambement Ungewitter donne la longueur maximale pour un meneau face au risque d’instabilité de type flambement en prenant un coefficient de sécurité de 10 sur la charge axiale critique provoquant le flambement, pour différents chargements ($P$, $P/2$ et poids propre seul). Le flambement est considéré :

selon la petite inertie (Knicken seitlich durch dans le tableau A), dans le cas où les barlotières ne s’opposent pas au mouvement dans le plan de la baie. En pratique cette vérification semble présenter peu d’intérêt, puisque justement les barlotières peuvent dans la plupart des cas s’opposer au mouvement latéral des meneaux dans le plan de la baie
selon la grande inertie (Knick. n. d. Tiefe durch dans le tableau A). Ungewitter remarque que le rapport $L_m/t$ est de l’ordre de 40 pour le coefficient de sécurité de 10, pour pouvoir porter le chargement maximum $P$ lié uniquement à la résistance en compression centré. Il ajoute que si la mise en œuvre était très soignée et le matériau de qualité irréprochable, il serait envisageable d’abaisser le coefficient de sécurité à 5, voir à 2.5, et ainsi le rapport $L_m/t$ être de l’ordre de 60 à 80 (sous réserve que le flambement selon la petite inertie soit empêché par les barlotières).

Résistance au vent Ungewitter considère que « le vent exerce sur un meneau une sollicitation similaire à une charge verticale sur une plate-bande. » (Ungewitter et Mohrmann, 1920, p.680). Il détermine pour une hauteur utile $t/2$ (demi-hauteur) ou $\frac{10}{36}t$ (hauteur du noyau central) la poussée verticale $D$ qui se développe dans un meneau sous la charge latérale $w=$120kg/m² correspondant au vent. Il vérifie que cette poussée $D$ est admissible du point de vue de la résistance de la pierre. Il est à noter que la poussée $D$ n’étant pas centrée, dans le cas où l’on considère le noyau central la contrainte sur le joint est le double de celle qui correspondrait à une poussée $D$ centrée. Ungewitter indique en légende du tableau A qu’il considère pour la résistance à la compression excentrée (qui n’est pas permanente mais ne se produit qu’en cas de tempête) le double de la résistance des matériaux donnée ci-dessus, soit respectivement 1,0MPa, 2,0MPa et 4,0MPa. Les deux effets s’annulant, cela permet à Ungewitter de comparer directement la poussée verticale $D$ à la résistance à la compression centrée $P$ (déduction faite du poids propre du meneau) dans le tableau A. Les résultats sont donnés dans deux tableaux pour une pression de vent $w=120$kg/m² :

Le tableau A donne les longueurs admissibles des meneaux en fonction de leur entraxe et en prenant une hauteur utile $\frac{10}{36}t$ correspondant au noyau central (de la section type utilisée par Ungewitter pour ses calculs).
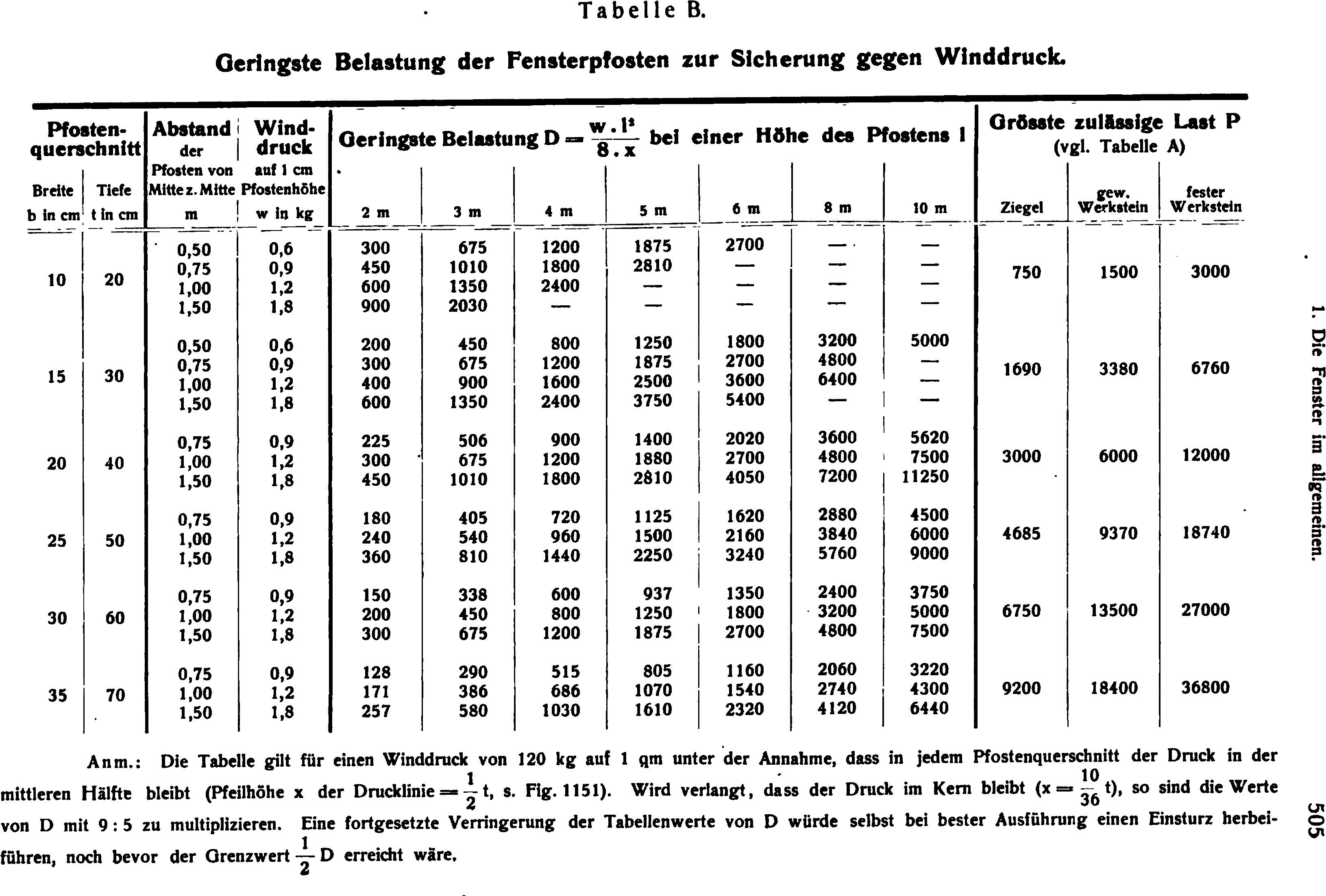
le tableau B donne la poussée verticale $D$ en fonction de l’entraxe des meneaux et en prenant une hauteur utile $t/2$. Il faut multiplier $D$ par $36/10/2=9/5=1.8$ pour obtenir le résultat plus conservatif correspondant à une hauteur utile de $\frac{10}{36}t$. Il faut vérifier que $D$ reste inférieur à la charge admissible en compression $P$ présentée dans le tableau A et qui est rappelée dans le tableau B. Ungewitter ajoute : « On this Table it may be stated, that the minimum loads given under $D$ suffice for well executed windows not too much exposed to storms, but with inferior execution and exposed location is required an increase of 9/4 or double, while on the other hand for especially protected windows the loads on the mullions may be also reduced. » (Ungewitter et Mohrmann, 1920, p.681)

La poussée verticale $D$ qui se développe dans le meneau en cas de vent doit être reprise par les charges verticales situées au-dessus du meneau (Ungewitter et Mohrmann, 1920, p.684-686). Selon Ungewitter, la situation la plus favorable se présente lorsque le réseau présente une masse suffisamment grande pour jouer ce rôle, mais cette disposition n’est pas systématique. Dans le cas contraire, il convient de s’assurer que la masse de l’arc et des maçonneries portées par l’arc de la baie (la partie supérieure du mur) est suffisante pour jouer ce rôle. Et réciproquement il faut vérifier que ces charges ne dépassent pas la capacité portante du meneau. Le phasage de construction du remplage (avant ou après la fermeture de l’arc de la baie) joue un rôle important dans les charges s’appliquant sur le meneau, même en l’absence de vent, de même que la différence de rigidité entre le remplage et le mur.

Fig 5: Tableau A, d’après Ungewitter et Mohrmann (1903, p.504)

Fig 6: Tableau B, d’après Ungewitter et Mohrmann (1903, p.505)

2.4 Reformulations et remarques

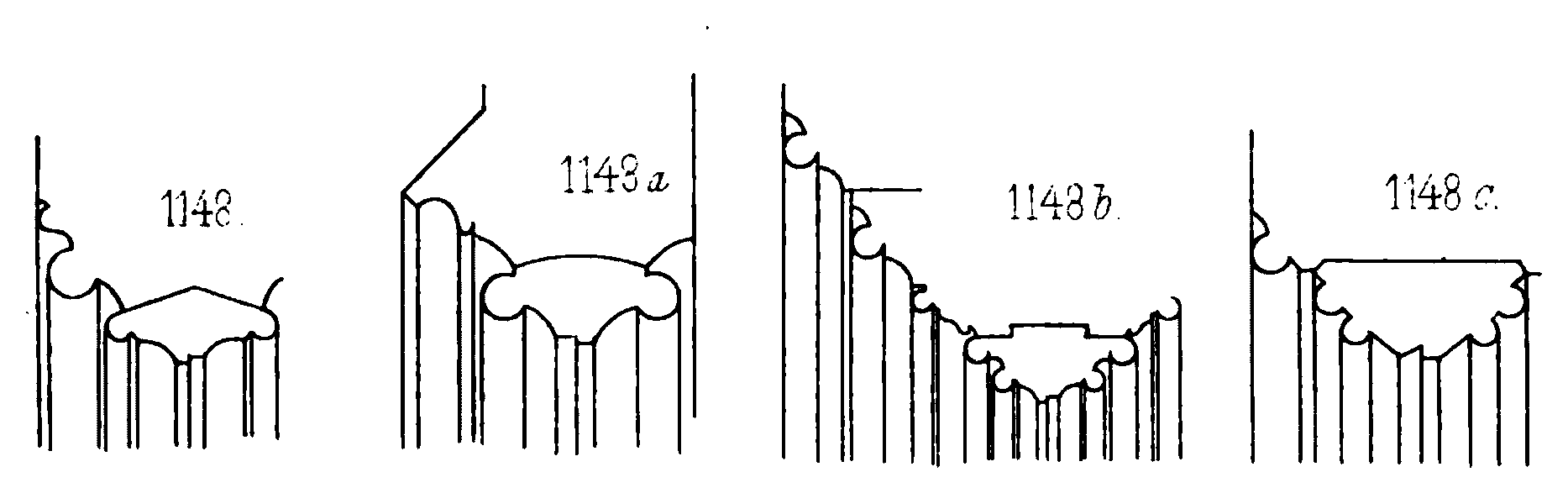
Les vérifications proposées par Ungewitter peuvent être reformulées et généralisées comme suit. Soit $\sigo $ la résistance admissible en compression des meneaux, $w$ la pression du vent (kg/m²), $e_m$ l’entraxe entre meneaux (m), $L_m$ la hauteur du meneau (de l’appui de la fenêtre à son chapiteau) (m), $D$ la poussée qui se développe dans un meneau sous l’effet du vent (kg), $G$ le poids propre du meneau additionné du poids propre du réseau prenant appui sur le meneau (kg) et $x=2W/A$ la hauteur du noyau central de la section (m) qui se déduit de l’aire $A$ et du module d’inertie $W$ de la dite section.

La résistance en compression centrée est vérifiée si la contrainte sous poids propre n’excède pas la résistance, soit : $$G/A<\sigo $$

La résistance du meneau sous l’effet du vent nécessite de se donner la poussée verticale $D$ générée par le vent dans le meneau fonctionnant comme une plate-bande, soit : $$D = \frac{ w e_m L_m^2 }{8 x}$$

Ungewitter utilise des valeurs particulières pour la hauteur du noyau central ($x=10/36 t$) liée à la géométrie simplifiée de la section du meneau utilisé dans ses calculs, mais rien n’empêche aujourd’hui de faire les calculs pour une section quelconque. Par ailleurs, l’hypothèse de limiter la hauteur utile de la plate-bande $x$ à la hauteur du noyau central est peut-être trop conservatrice, mais nous la conservons par commodité pour la suite des calculs.

Connaissant l’effort axial dans le meneau $N=D + G/2$, ainsi que le moment de flexion $M=\frac{1}{2}xD$, on en déduit la contrainte maximale $\sigma_{max}$ atteinte dans le meneau et on la compare à la résistance admissible instantanée (double de la résistance centrée de long terme selon Ungewitter) : $$\sigma_{max}=N/A+M/W<2\sigo $$

Enfin, on vérifie que l’effort axial dans le meneau $N=D + G$ est inférieur à la charge critique de flambement $N_{cr}$ suivant la grande inertie (le flambement suivant la petite inertie étant supposé bloqué par les barlotières). $$N_{cr}=\pi{}^2 \frac{E I}{sL_m^2}$$ où $s$ est le coefficient de sécurité considéré, pris égal à 10 par Ungewitter.

Notons que le calcul du flambement est la partie la moins satisfaisante du raisonnement présenté par Ungewitter. En effet ce dernier utilise des modules d’Young qui ne prennent pas en compte l’influence des joints (il prend par exemple E=25GPa pour un calcaire tendre). La raideur du meneau est donc surestimée (et la charge critique jusqu’à laquelle le meneau peut résister est également surestimé dans les mêmes proportions). Cela est compensé par le coefficient de sécurité $s=10$ qui est lui aussi probablement excessif (nota : ne pas confondre ce coefficient de sécurité 10 sur la charge critique, et le coefficient de sécurité 10 sur les contraintes). De plus la vérification du flambement présenté par Ungewitter ne prend pas en considération l’intéraction entre l’effort axial ($D$), le moment de flexion ($M$) du au vent et la pression du vent elle-même $w$. L’effort axial conduisant au flambement du meneau en présence de vent semble devoir être nécessairement inférieur à la charge critique d’Euler calculé par Ungewitter.

L’intégration du flambement au raisonnement nécessite donc de pousser un peu plus loin l’analyse, ce qui est alors difficilement réalisable de façon analytique. En particulier, il n’est pas possible d’utiliser les abaques existantes (par exemple l’abaque proposée par Como (2013, p.412) ne serait pas adapté car elle n’intègre pas d’effort $w$ et sous-estime donc l’effort critique) pour évaluer l’effort critique réel. L’outil numérique (calcul aux éléments finis, modèle non linéaire pour détecter charge critique du meneau soumis à $D$ et $w$) s’avère utile dans ce cas.

Au final, la vérification des meneaux sous la pression du vent proposée par Ungewitter revient à étudier une plate-bande en considérant un coefficient géométrique de sécurité de 3 (dans le cas où $x$ est égal à la hauteur cas du noyau central) et en considérant une résistance à la compression double de la résistance usuelle, car les pressions extrêmes du vent ne se produisent que rarement, et en vérifiant que l’effort axial maximum dans le meneau ne peut pas générer de flambement. On note que Ungewitter n’applique pas de coefficient de sécurité sur la pression du vent, car la sécurité est déjà contenue dans le facteur 10 appliquée à la résistance en compression (il s’agit d’une méthode de calcul avec contraintes admissibles, qui se distingue de la méthode actuelle des coefficients partiels utilisés notamment dans les eurocodes).

Il conviendra également de vérifier l’absence de risque de glissement au niveau du pied et de la tête du meneau, soit en vérifiant l’angle de la force par rapport à la normale au joint, soit en vérifiant la présence d’un système (goujon ou autre) empêchant le risque de glissement. On remarquera par analogie avec les plates-bandes à joints verticaux (stable d’un point de vue théorique, mais jamais utilisée en pratique en raison du risque de glissement au moindre tassement des maçonneries), la supériorité des systèmes où des goujons empêchent le glissement, et en particulier en partie haute du remplage.

Notons que pour toutes ces vérifications, un des paramètres essentiel est la hauteur libre du meneau $L_m$, ou plus exactement son élancement géométrique $L_m/t$. Le réseau (partie du remplage situé au-dessus des meneaux) est implicitement supposé suffisamment résistant et rigide par Ungewitter pour qu’il forme un appui horizontal stable pour la tête du meneau.

La hauteur libre du meneau conditionne l’effort axial minimal qui doit pouvoir se développer dans les meneaux (dépendance en $L_m^2$), ainsi que l’effort axial admissible en flambement (dépendance en $L_m^2$ également, avec les réserves évoquées précédemment). Ungewitter indique que les réseaux commencent progressivement de plus en plus bas lors de l’époque gothique, diminuant ainsi de fait la hauteur libre des meneaux (1152 1153 sur figure 7). De plus, des croisillons ou arcades pouvaient être ajoutés en partie basse des réseaux, pour diminuer encore une fois la hauteur libre des meneaux (1154 1555 1555b 1555c sur figure 7).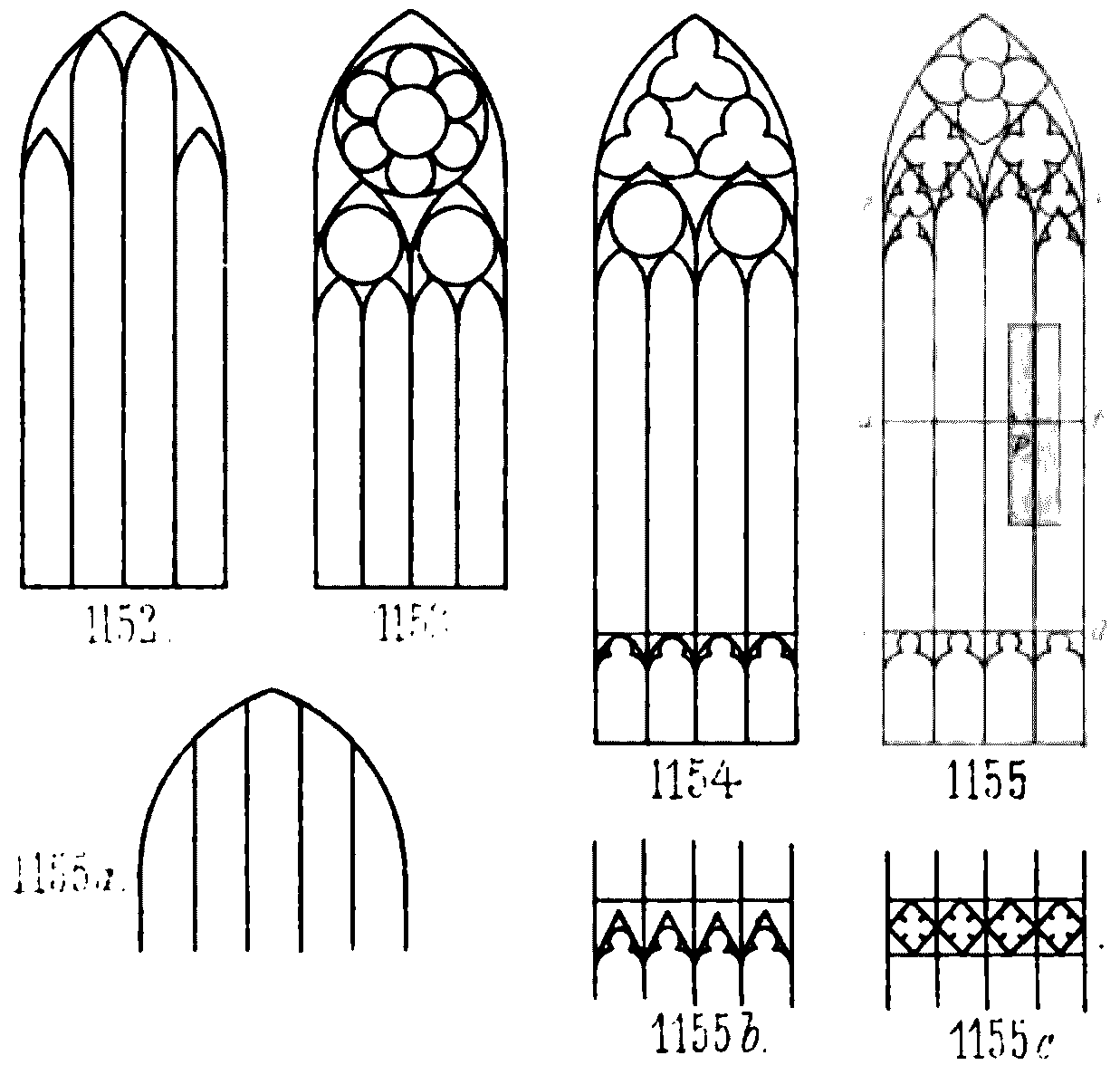

Fig 7: Hauteur libre des meneaux variables pour baies de même hauteur, d’après Ungewitter et Mohrmann (1903, Tafel CXIV)

Heyman (2002) présente également les rudiments de la vérification des meneaux, et étend ses vérifications aux roses. Les vérifications proposées par Heyman restent moins détaillées que celles de Ungewitter, et en particulier il ne mentionne pas la problématique du flambement qui est le phénomène critique pour la stabilité des meneaux des grandes baies.

3 Les barlotières

3.1 Typologie des barlotières

Les panneaux de vitrail, pour des raisons de rigidité, ont une hauteur comprise entre 50 et 100cm (Ungewitter et Mohrmann, 1920, p.670). Cette hauteur conditionne l’entraxe des barlotières qui doivent porter les panneaux de vitrail, qui est égale à la hauteur des panneaux de vitrail. Par ailleurs, la longueur des barlotières ne dépasse généralement pas 125 à 150cm dans les édifices gothiques selon Ungewitter et Mohrmann (1920, p.674), même s’il doit nécessairement exister des exceptions. La longueur des barlotières peut être bien plus longue dans les édifices de l’Époque Moderne où les remplages tendent à disparaître.

Les barlotières sont composées de barres de section rectangulaires, de 25 à 40 mm de haut, et 8 à 15 ou plus d’épaisseur (c’est-à-dire la dimension qui travail pour résister au vent ; Ungewitter et Mohrmann (1903, p.498), Ungewitter et Mohrmann (1920, p.672)). Les sections peuvent atteindre 50x50mm pour certaines baies exceptionnelles.

Les barres sont scellées de 40 à 80mm dans les jambages et les meneaux selon Ungewitter.

Si on s’intéresse au caractère traversant ou non à travers les meneaux, on peut redécouper les barlotières en 3 catégories :

barlotière non traversante (des meneaux)
barlotière traversante (d’un meneau, de tous les meneaux etc.)
barlotière traversante et assemblée aux barlotières des travées adjacentes (barlotières-tirants). Les barlotières-tirants forment alors un chaînage (L’Héritier et al., 2012).

3.2 Vérification de la résistance et rigidité

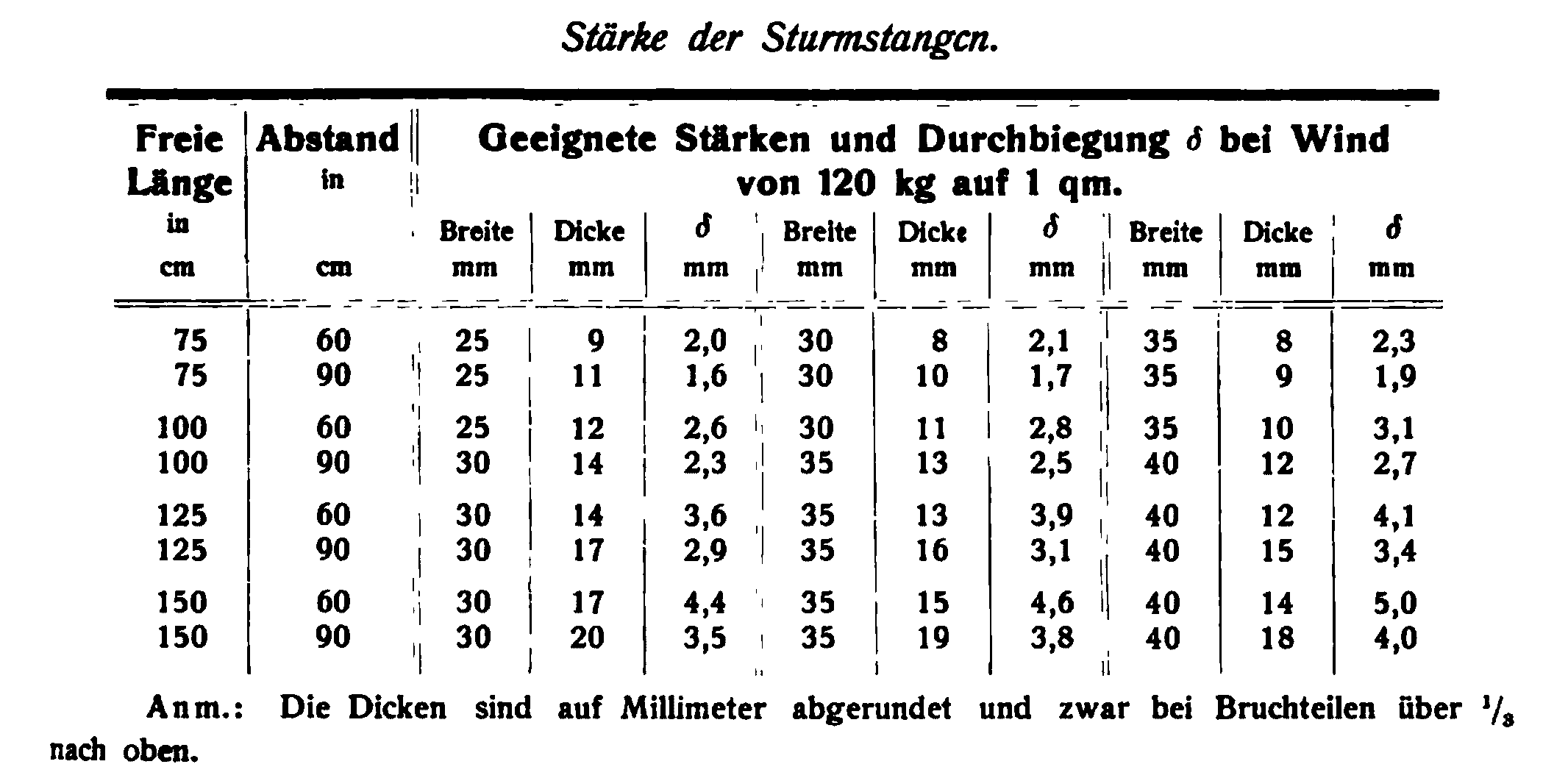
Il est à noter que nous n’avons pas abordé le rôle des barlotières jusqu’à présent, si ce n’est pour bloquer le flambement des meneaux selon leur petite inertie (flambement dans le plan de la baie). Dans les calculs conduits par Ungewitter, les meneaux en pierre assurent la résistance globale aux efforts de vent, les barlotières n’ont qu’un rôle de portance locale de meneau à meneau.

Les barlotières supportent la charge verticale des panneaux de vitraux (charge faible, de l’ordre de $10kg/m^{2}$, soit de l’ordre 5 à 10 kg/ml en général), et la charge horizontale de la pression du vent (Ungewitter considère $120kg/m^{2}$, soit 10 fois plus que le poids des vitraux) uniquement de meneau à meneau (ou de meneau à jambage).

Pour vérifier leur résistance au vent, Ungewitter fournit un tableau (voir fig 8) de dimensions acceptables pour les barlotières pour différentes longueurs et portées de ces dernières en considérant :

un vent de $120kg/m^{2}$
que les barlotières se comportent comme des barres encastrées dans leurs appuis (rotation des barres bloquée par la maçonnerie)
que le métal a une résistance admissible égale à 100MPa

Ungewitter note la bonne concordance des dimensions obtenues par ces hypothèses et les dimensions qu’il a observé en pratique sur les remplages existants. On constate que les déformations données par Ungewitter et jugées admissibles par Ungewitter, correspondent à peu près à un critère de flèche du 1/300e de la portée libre.

Ungewitter ajoute qu’on ne peut cependant pas garantir un encastrement parfait des barres (au sens blocage des rotations aux appuis), et qu’il convient donc d’augmenter l’épaisseur des barres (dans le plan horizontal) de 1/5e pour conserver des contraintes inférieures à 100MPa. Il remarque que ces barres surépaissies mais libres en rotation à leurs extrémités présentent néanmoins une flèche 3 fois plus importante que celles encastrées.

3.3 Reformulation et remarques

On peut reformuler l’approche d’Ungewitter comme suit. On ajoute aux notations déjà présentées précédemment : $\sigma_s$ la résistance admissible du métal, $e_b$ l’entraxe entre barlotières (m), $L_b$ la portée libre des barlotières entre deux meneaux (m), $I_s$ et $W_s$ le moment quadratique et le module d’inertie de la barlotière dans le sens du vent.

Les critères finaux d’Ungewitter utilisent une contrainte admissible de 100MPa et une flèche admissible (non explicité mais déduite de son exposé) de 1/100e de la portée, dans le cadre d’un calcul des barlotières considérées comme des barres appuyées de meneaux à meneaux (avec rotation libre aux appuis).

La flèche de la barlotière $f$ doit être inférieure à $L_b/100$. $$f=\frac{5}{384}\frac{w e_b L_b^4}{E_s I_s}$$

La contrainte de la barlotière $\sigma $ doit être inférieure à $\sigma_s=100\text{MPa}$ $$\sigma = \frac{1}{8}\frac{w e_b L_b^2}{W_s}$$

Ungewitter n’applique pas de coefficient de sécurité sur la pression du vent, car un coefficient de sécurité important est déjà pris sur la résistance du métal.

Bien que ce calcul considère que les barlotières sont composées de barres discontinues, c’est-à-dire de petites barres qui ne franchissent que la portée libre entre deux meneaux, les barlotières peuvent être en réalité continues (cf supra). Néanmoins Ungewitter remarque que généralement, les dimensions des barlotières ne sont pas suffisantes pour jouer un rôle porteur à elles-seules (sans considérer les meneaux). Viollet-Le-Duc (1863) fait la même observation en introduction à son article sur les meneaux : « Mais vers la fin du XII^e siècle, au moment de l’adoption du système de l’architecture dite gothique, les fenêtres venant à s’agrandir, il fallut disposer dans leur surface vide des séparations en pierre pour maintenir les vitraux ; car les armatures en fer, difficiles à fabriquer, flexibles, ne présentaient pas une résistance suffisante à l’effort du vent. »

Fig 8: Stärke der Sturmstangen
d’après Ungewitter et Mohrmann (1903, p.499)

3.4 Meneaux élancés et fortes barlotières

Ungewitter remarque que lorsque les meneaux deviennent trop élancés ($L_m/t$ grand), alors ils ne peuvent plus assurer seuls le rôle porteur. Il devient nécessaire de considérer l’aide fournie par les barlotières pour permettre d’expliciter la stabilité des meneaux.

Il critique cette disposition (où les meneaux ne sont plus stables par eux-mêmes) en raison du risque que pose la corrosion de ces barlotières, et parce que la trop faible raideur des barlotières entraîne la fissuration des joints lors des coups de vent (Ungewitter et Mohrmann, 1920, p.673,676).

4 Conclusion

L’approche calculatoire des meneaux et des barlotières présentée par Ungewitter et Mohrmann (1903) reste utile aujourd’hui et permet de comparer très rapidement, sans nécessiter de modélisation complexe, les remplages de différentes baies entre elles. Il s’agit également d’un exercice de compréhension du fonctionnement mécanique de ces objets, qui a une valeur pédagogique en soi indépendamment des résultats numériques.

On pourra objecter du manque de considération de l’interaction entre les barlotières et les meneaux pour avoir une approche plus fine du comportement mécanique. Cependant, le raisonnement d’Ungewitter est parfaitement admissible pour démontrer la stabilité du remplage. A ce sujet, Heyman (2002) écrit « En fait le problème est hyperstatique à l’extrême, et le mieux que puisse faire l’ingénieur structure dans ce genre de situation est de prendre des hypothèses ‘raisonnables’ pour quelques-uns des paramètres entrant dans les calculs. Ces hypothèses n’invalident pas la méthode, et c’est un fait que les ingénieurs structures ont toujours travaillé de cette manière, et se sont appuyés, sans le savoir le plus souvent, sur le confort des théorèmes de l’analyse limite ».

Certes la prise en compte du flambement parait, du fait des moyens de calcul facilement accessibles aujourd’hui, assez limitée, mais ce point pourra justement faire l’objet d’une étude plus poussée si nécessaire au cas par cas. Des méthodes de calculs plus poussées ont également été appliquées et publiées plus récemment aux remplages ou aux roses, comme l’utilisation de la méthode des réseaux de forces aux roses (Block, 2009), ou la méthode des éléments finis à un remplage (Barthel et al., 2003).

Pour approfondir l’étude du mode constructif des remplages nous conseillons, outre Ungewitter, la lecture suivante : Viollet-Le-Duc (1863).

Article mis en ligne le : 27/01/2023.
Révisé le : 23/02/2013.

Sur l’auteur :

Mathias Fantin est ingénieur structure et docteur en architecture, et il travaille sur la restauration des monuments anciens. Il a fondé en 2014 Bestrema, un bureau d’études structures spécialisé dans ce domaine.

Ces autres articles pourraient également vous intéresser :

Résistance et stabilité des remplages -
Vérification de la résistance et stabilité des remplages, supports en pierre des vitraux dans les édifices gothiques.
La géométrie des voûtes -
La géométrie des voûtes renvoie à deux concepts : la forme de l’intrados et l’appareil. Étude des correspondances et divergences entre les deux.
Étude des rapports entre stéréotomie et … -
Présentation d’une thèse de doctorat en architecture explorant l’influence de la coupe des pierres sur la stabilité des voûtes clavées.

Bibliographie

[Barthel et al. 2003]: BARTHEL, R., L. SCHIEMANN et M. JAGFELD. 2003, Static analysis and evaluation of the construction system of a gothic « choir-window » consisting of a filigree tracery and slender stone rips, dans Proceedings of the first international congress on construction history, Madrid, p. 333-340.
[Block 2009]: BLOCK, P. 2009, Thrust Network Analysis : exploring three-dimensional equilibrium, thèse de doctorat, Massachusetts Institute of Technology, Dept. of Architecture. URL http://dspace.mit.edu/handle/1721.1/49539.
[Como 2013]: COMO, M. 2013, Statics of historic masonry constructions, Springer, Berlin; New York.
[Heyman 2002]: HEYMAN, J. 2002, Rose Windows, dans New Approaches to structural mechanics, shells and biological structures, Kluwer Academic Publishers, Dordrecht, p. 165-177.
[Huerta Fernández 2006]: HUERTA FERNáNDEZ, S. 2006, Geometry and equilibrium: The gothic theory of structural design, Structural Engineer, vol. 84, 2, p. 23-28. URL http://oa.upm.es/701/.
[L’Héritier et al. 2012]: L’HéRITIER, M., P. DILLMANN, A. TIMBERT et P. BERNARDI. 2012, The role of iron armatures in gothic constructions : Reinforcement, consolidation or commissioner’s choice, dans Nuts & Bolts of Construction History, Picard, Paris. URL http://www.icch-paris2012.fr/.
[Pérouse de Montclos 2007]: PéROUSE DE MONTCLOS, J.-M. 2007, Architecture : méthode et vocabulaire, 6e é#233;d., Impr. nationale : Ed. du patrimoine, Paris.
[Ungewitter et Mohrmann 1903]: UNGEWITTER, G. G. et K. MOHRMANN. 1903, Lehrbuch der gotischen Konstruktionen, vol. 2, 4e é#233;d., Tauchnitz, Leipzig. URL http://www.archive.org/details/lehrbuchdergoti01mohrgoog.
[Ungewitter et Mohrmann 1920]: UNGEWITTER, G. G. et K. MOHRMANN. 1920, Manual of Gothic Construction, 3e é#233;d., Illinois. URL http://archive.org/details/5631513.
[Viollet-Le-Duc 1863]: VIOLLET-LE-DUC, E. 1863, Meneau, URL https://fr.wikisource.org/wiki/Dictionnaire_raisonn%C3%A9_de_l%E2%80%99architecture_fran%C3%A7aise_du_XIe_au_XVIe_si%C3%A8cle/Meneau.

Notes :

¹ Ungewitter et Mohrmann (1920, p677) relève à ce sujet certaines proportions pour le meneau (l’épaisseur du meneau valant le tiers ou 4/10 de l’épaisseur du mur à une certaine époque), tout en soulignant la limite de cette règle de proportion basée sur l’épaisseur du mur et non la hauteur libre du meneau.