1 Introduction
La stabilité des encorbellements, en particulier des corbeaux et des consoles, met en jeu à la fois des notions d’équilibre et de résistance. Adam en donne une description dans son livre La construction romaine : matériaux et techniques, qui résume en quelque lignes la simplicité apparente du problème :Statiquement, l’encorbellement est constitué d’une pièce possédant une partie en appui et une partie en saillie, la première devant être suffisamment pesante pour éviter la bascule ; la seule précaution des constructeurs consiste donc à charger la partie en queue dont la longueur dont être supérieure à la saillie. Il convient également d’estimer empiriquement, les limites de résistance du matériau, afin de s’opposer par une épaisseur suffisante à sa rupture sous l’effet de la flexion. Adam 1989 [1,p.179]Un corbeau dont la queue n’est pas chargée ne peut avoir une saillie supérieure à la longueur de sa queue (voir l’article d’introduction aux encorbellements pour la définition de ces termes). Bien souvent, la saillie du corbeau est bien inférieure à la queue pour des questions de sécurité. Il existe de nombreuses méthodes différentes pour permettre l’augmentation de la saillie possible pour un encorbellement. La présentation du fonctionnement statique des encorbellements que nous aurons vu dans la première partie, permettra ensuite de mettre en avant les moyens particuliers employé par les constructeurs anciens pour assurer la stabilité des encorbellements. Nous relierons à chaque fois ces différentes pratiques au gain en équilibre ou en résistance correspondant. Nous verrons que ces dispositifs constructifs sont assez souvent invisibles pour l’observateur extérieur. Nous verrons enfin rapidement les méthodes qui étaient utilisées pour choisir les dimensions à donner aux corbeaux et consoles qui composent les encorbellements. Rappelons pour clore cette introduction les définitions que nous avons introduit lors du précédent article sur les encorbellements pour simplifier et clarifier les descriptions du point de vue structurel. Nous utiliserons des étoiles pour distinguer les termes définis ci-dessous des termes généralement utilisé dans le vocabulaire de l’architecture :
- Un corbeau* est une pierre monolithe portant une charge en surplomb par rapport au nu du mur.
- Une console* est un assemblage de corbeaux* superposés, formant un système portant en encorbellement.
2 Equilibre et résistance des encorbellements
Notre présentation de l’équilibre et de la résistance des encorbellements s’appuie en grande partie sur la présentation de la stabilité des corbeaux dans l’architecture gothique par Ungewitter (1901 [16]). Nous indiquerons à chaque fois les références de l’édition allemande de 1901 [16], et la référence correspondante dans la traduction anglaise de 1920 [17].2.1 Cas simple du corbeau*
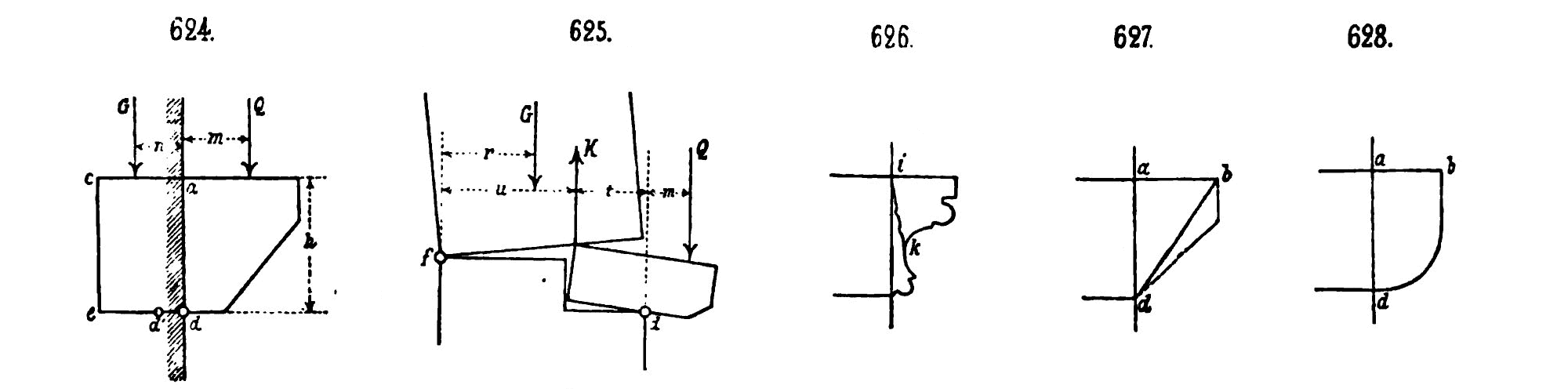
Considérons pour débuter le cas le plus simple : celui d’un corbeau* de poids $G$ en appui simple sur un mur, et qui n’est chargé que par une surcharge d’exploitation $Q$. La position de l’origine des axes pour le calcul des moments est choisie au niveau du nu du mur au point $d$. Ce point correspond à l’arête du mur sur lequel repose le corbeau*. Les bras de levier respectifs de $G$ et $Q$ par rapport à $d$ sont notés $n$ et $m$. Le corbeau* est en équilibre si le moment résistant $n\cdot G$ est supérieur au moment sollicitant de $m\cdot Q$ (Fig. 1).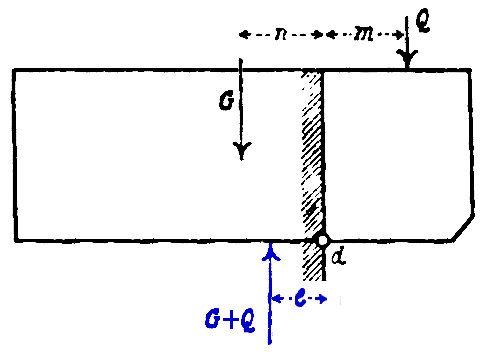
Fig 1: Equilibre d’un corbeau* en appui simple sur un mur
schéma adapté d’un dessin de Ungewitter 1901 [16]
schéma adapté d’un dessin de Ungewitter 1901 [16]
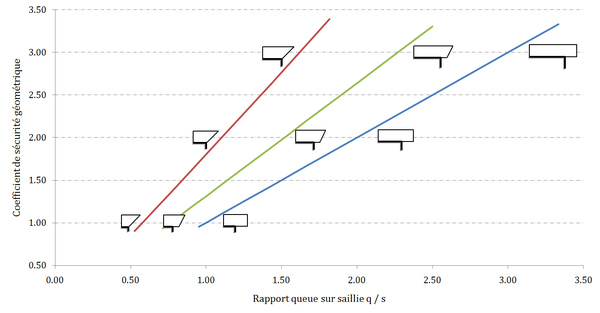
Fig 3: Abaque des coefficients de sécurité géométrique des corbeaux non chargés, en fonction du rapport queue sur saillie
- la résistance au cisaillement est généralement inférieure à celle en flexion ;
- si ces deux résistances étaient égales, le mode de rupture en cisaillement n’est plus dimensionnant par rapport au mode de rupture en flexion, dès que la saillie de la charge $Q$ dépasse le sixième de la hauteur du corbeau*2.
La force oblique de la voûte [« Wölbdruck »] passe habituellement dans le mur à une grande distance au dessus de la naissance de l’arc. Le chapiteau d’un petit pilier ou d’un corbeau n’est pas sollicité par la force oblique de la voûte, de telle manière que ces éléments ont un rôle architectonique plutôt qu’un rôle porteur. Au contraire, les contraintes dans un corbeau sous les poutres, solives, etc. est suffisamment important pour nécessité une observation plus poussée. Ungewitter 1901 [16,p.239] 1920 [17,p.332]
2.2 Equilibre et résistance des consoles*
Nous avons vu ci-dessus que la stabilité d’un corbeau* se vérifiait en considérant successivement son équilibre puis sa résistance, en fonction des charges qui s’appliquent à ce dernier, et à la surface disponible pour son appui sur le mur inférieur. La stabilité des consoles*, formées par définition de plusieurs corbeaux*, est vérifiée en considérant successivement la stabilité de chaque corbeau*, de haut en bas. En général, l’assise qui présentera le plus petit coefficient de sécurité vis-à-vis du basculement, et donc le plus grand risque, sera l’assise la plus basse. Dans ce cas les résultats correspondant d’une part à une console*, et d’autre part à un corbeau* ayant les mêmes contours extérieurs que la console*, seront identiques du point de vue de l’équilibre. Cependant, cette similarité n’est pas vraie du point de vue de la résistance. Les consoles* peuvent présenter des contraintes plus importantes que le corbeau* équivalent.2.3 Encorbellements armés
Lorsque le poids du corbeau* et son contrepoids supérieur à l’aplomb du mur n’est pas suffisant pour assurer l’équilibre, les constructeurs prévoyaient des dispositifs spéciaux pour appliquer de nouvelles charges résistantes sur le corbeau* et ainsi le stabiliser. Parmi ces dispositifs, les tirants, crampons ou agrafes en fer tiennent une place de choix. Nous reviendrons sur ces dispositifs plus loin dans cet article. Du point de vue de l’équilibre, ces systèmes introduisent soit de nouvelles charges verticales, soit de nouvelles charges horizontales. La considération de ces charges résistantes, et surtout du moment qui leur correspond, permet d’augmenter la stabilité des systèmes considérés du point de vue de l’équilibre.3 La recherche de l’équilibre
Que l’encorbellement ait pour but l’embellissement d’une façade (corniches), l’ajout d’une fonction (mâchicoulis), ou l’augmentation des surfaces accessibles (quais), son constructeur devait toujours tenir compte de l’équilibre, qui limitait l’ampleur possible de la saillie. Pour augmenter autant que possible la saillie, ou améliorer la stabilité d’un type de construction qui posait problème, deux principes simples sont employés. La partie qui se trouve hors de l’aplomb du mur est allégée, et/ou la partie qui se trouve à l’aplomb du mur est alourdie. Ces deux principes trouvent différentes traductions suivant les éléments considérés (balcon, corniche, etc.), la date de construction, le lieu de construction etc. Nous explorons dans cette partie ces principes stabilisateurs. Nous nous intéresserons également rapidement à la question des matériaux et de leur influence sur l’équilibre.3.1 Contrepoids
Le concept de contrepoids est à la base de la compréhension de l’équilibre des constructions en encorbellement. Enlart écrit ainsi :L’encorbellement se maintient sur le vide grâce à un contrepoids : il faut que la queue des pierres qui le composent soit assez lourde par elle-même ou assez chargée par d’autres maçonneries pour que ce poids neutralise la pesanteur et par conséquent la tendance à tomber de la partie en surplomb ; la queue ou sa charge, forme, en d’autres termes, le contre-poids qui empêche l’encorbellement de basculer. Enlart [10,p.19]Pour augmenter le contrepoids d’un corbeau, le moyen le plus simple est donc d’augmenter la queue de ce dernier. Cet effet est bien visible sur la figure 3 que nous avons présenté ci-dessus. Il est même possible d’allonger la pierre en encorbellement pour dépasser le nu intérieur du mur, pour exploiter au maximum l’effet du contrepoids fournit par la queue du corbeau (voir Toussaint 1828 [15,pp.229-230] dans le cas des corniches). Ce contrepoids intrinsèque au corbeau n’est toutefois souvent pas suffisant. Les contrepoids additionnels mentionnés par Enlart sont alors placés au-dessus de la queue de l’encorbellement. Ils peuvent également être placés sous l’encorbellement. Contrepoids supérieur Pour augmenter la stabilité, des contrepoids peuvent être placé à l’aplomb du mur, au dessus des corbeaux ou consoles. Suivant, la position de la construction en encorbellement dans le bâtiment, le contrepoids peut prendre différentes formes :
- les trumeaux du mur, notamment pour les consoles et dalles de balcons situés sous ces derniers. L’encyclopédie des métiers souligne qu’il faut attendre que les trumeaux chargent suffisamment les consoles lors de la construction pour permettre la dépose des étaiements utilisés lors de la pose de la dalle du balcon (1991 [2,p.605]) ;
- les acrotères, si ces dernières sont placées en retrait par rapport à la saillie de la corniche ;
- les murets des courtines côté intérieur (Fig. 5). Les parapets portant côté extérieur ont évidemment l’effet inverse ;
- les dalles de couverture des portiques de l’architecture du XVIIIe (Fig. 6), dont l’appui sur les encorbellements peuvent éventuellement se trouver en dehors de l’aplomb du mur du côté opposé à l’encorbellement, pour augmenter encore l’effet de ce contrepoids.
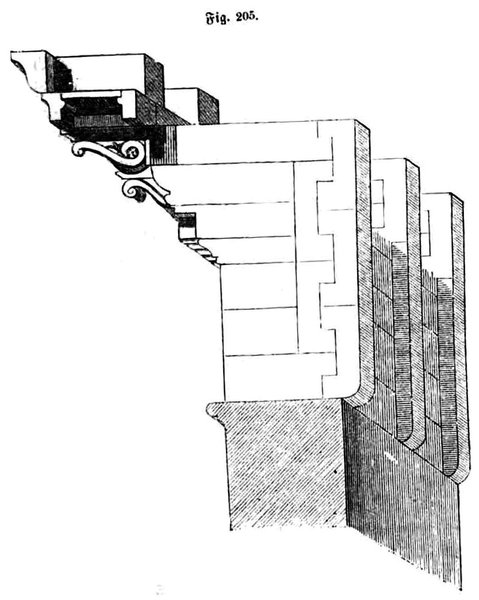

Fig 7: Palazzo Strozzi à Florence
à gauche : d’après Breymann 1868 – scanné par la BSB
à droite : d’après Planat 1888 [14] – INHA
à gauche : d’après Breymann 1868 – scanné par la BSB
à droite : d’après Planat 1888 [14] – INHA
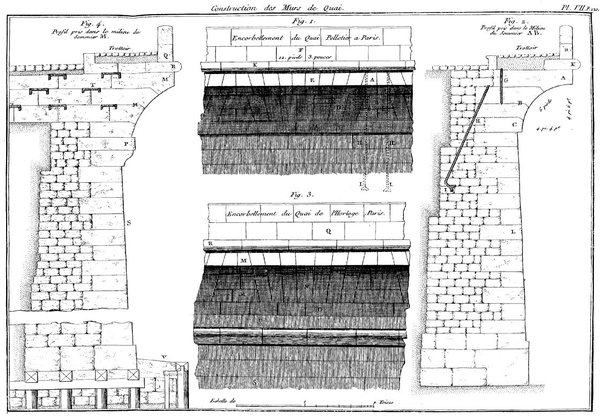
Fig 8: Encorbellement du mur du Quai de l’Horloge et du Quai Pelletier, à Paris 1769 [12] – scanné par la BNF
3.2 Elégissements, claire-voies, amaigrissement des profils
La création de vides au sein de la structure en encorbellement, ou l’amaigrissement de son profil sont deux moyens pour alléger la partie en saillie et favoriser l’équilibre. Les termes utilisés pour désigner ces vides peuvent être élégissement et élégir, ou bien plus simplement évidement5. Les élégissements concernent l’encorbellement lui-même, ou bien les structures portées par l’encorbellement. Dans le premier cas, la forme triangulaire ou trapézoïdale des corniches leur donne un avantage très net en terme de stabilité. On pourra comparer les encorbellements rectangulaires et les encorbellements à saillie triangulaire donnés sur la figure 3 ci-dessus. A saillie égale, la queue nécessaire pour obtenir le même degré de stabilité pour une corniche à profil triangulaire est presque deux fois moindre que celle nécessaire pour une corniche à profil rectangulaire. Acrotères, créneaux et garde-corps sont autant de murs maçonnés qui sont parfois placés au delà du nu du mur sur l’extrémité d’une corniche ou d’un balcon. Ces charges jouent très défavorablement à l’encontre de l’équilibre de l’encorbellement. L’allègement de ces murs est souvent essentiel à la stabilité. Ils sont alors à claire-voies. D’Aviler note à propos des entrelas d’appui des bâtiments Gothiques : « Les Architectes de ces temps-là se plaisoient aussi à les faire porter à faux sur l’extremité d’une corniche, ainsi que les Creneaux & Machecoulis des vieux Châteaux. » 1691 [7,p.324]. Viollet-le-duc consacre un article complet aux balustrades, mais les informations qu’il donne concernent essentiellement leur ornementation. Notons enfin les élégissements créés au pied des tourelles pour éviter de charger inutilement en maçonnerie les parties situés hors de l’aplomb des murs inférieurs (voir article Tourelle de Viollet-le-duc, qui décrit ces vides).3.3 Matériaux
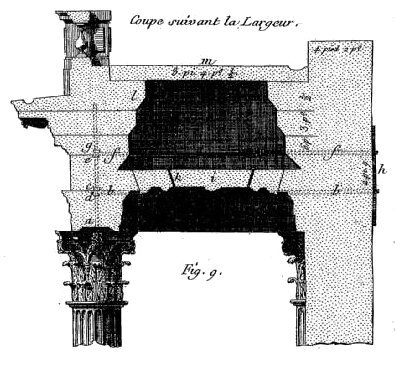
La question des matériaux utilisés pour la construction des encorbellements semble assez peu documentée, en ce qui concerne leur influence sur l’équilibre et de la résistance. Viollet-le-Duc évoque rapidement l’influence des matériaux locaux disponibles sur la forme des corniches (1860 [19]). Les sources qui font référence aux matériaux évoquent principalement la durabilité des matériaux (notamment dans le cas des corniches), mais pas leur résistance ou leur poids volumique. En règle générale, les sources indiquent que les pierres dures doivent être utilisées pour les parties supérieures des encorbellements exposés aux eaux de pluies (e.g. cimaises), et les pierres tendres peuvent être utilisées pour les parties abritées. Charue et al. soulignent à juste titre que la maçonnerie était « d’avantage choisie et mise en place plus pour sa résistance aux agents climatiques que pour sa capacité de travail en console » (1984 [3,III.67]). En effet la maçonnerie (pierre, brique, etc.) est moins adaptée au travail en flexion que le bois et le métal. Il est évident qu’il y a un intérêt à construire les acrotères, garde-corps, créneaux etc. qui portent à faux sur les corniches et balcons avec des pierres plus légères que celles des corbeaux et consoles, cet intérêt étant diminué par la faible durabilité de ces pierres tendres. Ce n’est d’ailleurs peut-être pas un hasard si l’utilisation des balcons en porte-à-faux se développe parallèlement à celle des garde-corps en serrurerie. Les garde-corps métalliques sont en effet beaucoup plus légers que les garde-corps à balustres qui ornent les balcons les plus anciens. L’utilisation d’un nouveau matériau pour les garde-corps a peut-être facilité le travail des constructeurs, en diminuant fortement les charges à reprendre sur l’extrémité des encorbellements des balcons. Les corniches en saillie ne sont pas toujours construites en pierre de taille. Elles peuvent être construites en moellon, notamment à Paris au XVIIIe siècle pour les maisons à loyer, ou en brique, dans le Nord et le Midi Toulousain (1991 [2,p.612]). En Provence, les génoises construites en tuiles canal sont un autre type de corniche non monolithe. Pour pallier au manque de cohésion de ces systèmes constructifs, l’usage de fers peut se révéler nécessaire. Dans le cas des corniches parisiennes construites en moellons, l’usage de ces fers était même réglementé au moins dès le XVIIIe siècle (Fig. 9). L’objectif est d’obtenir une construction aussi monolithe que possible. Les encorbellements construits en petits éléments de maçonnerie (ou de couverture dans le cas des génoises) sont généralement réservés aux structures recevant peu de charges, comme les corniches, pour lesquelles les problématiques de résistance sont peu importantes. L’estimation de la stabilité de ces constructions se réduit alors à une problématique d’équilibre.4 Evolution des techniques de dimensionnement
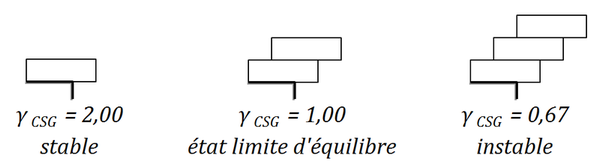
4.1 Proportions et principes de bonne construction
Pour d’autres constructions, comme les voûtes et des piédroits, il existe des sources écrites de la période gothique qui détaillent les proportions à donner aux contreforts, aux murs, aux nervures, en fonction de la portée de la voûte considérée (Huerta 2006 [11]). Ces proportions découlent de règles géométriques simples. Il est probable que les constructeurs anciens disposaient de règles comparables pour les constructions en encorbellement, pour choisir la hauteur ou la queue des consoles par exemple. Nous supposons que ces règles étaient exprimées en fonction de la saillie. Par ailleurs, ces règles étaient probablement accompagnées par d’autres traditions sur le type de matériau à employer, et sur la manière de le mettre œuvre. Si nous conjecturons l’existence de règles de proportions, nous n’avons cependant pas de détail à donner concernant le contenu de ces règles. L’observation des consoles des balcons par exemple, indique qu’il peut exister des variations régionales notables suivant la qualité du matériau disponible localement. On trouve ainsi en Corse du Sud des corbeaux* en granit bien plus élancées que les corbeaux* en calcaire que l’on trouve à Paris (voir ces articles sur les balcons en Corse du Sud et à Paris). Les règles géométriques de proportions variaient probablement suivant les régions. Aujourd’hui, une règle géométrique est parfois mentionnée par les maçons pour l’équilibre des consoles : 2/3 de queue pour 1/3 de saillie. Cette règle est mentionnée par exemple dans l’encyclopédie des métiers (1991 [2,pp.604,613]). L’origine de cette règle n’est pas connue. Limites des règles de proportions Les règles géométriques de proportion sont cependant insuffisantes pour garantir la stabilité des consoles. Prenons un exemple. L’application de la règle des 2/3 1/3 à un corbeau* non chargé conduit à une structure ayant un coefficient de sécurité géométrique de 2, supérieur à 1, donc la structure est stable. Cependant pour un corbeau* chargé sur sa saillie, il n’est pas possible de donner un coefficient de sécurité géométrique : cette situation peut-être stable ou instable suivant l’intensité de la charge. Par ailleurs, il est possible de construire des consoles* instables à partir d’une superposition de corbeaux* respectant tous la règle des 2/3 1/3 (Fig. 11). Des dispositifs complémentaires, comme les tirants et agrafes en métal, dont nous avons vu des exemples ci-dessus, entraient également dans la constitution des systèmes en encorbellement. Nous n’avons pas trouvé d’indication sur les règles ou traditions qui permettaient aux constructeurs anciens de savoir que les règles de proportion était insuffisantes dans les cas considérés, et nécessitaient donc l’application de dispositifs complémentaires. Nous avons montré ci-dessus le problème posé par les règles géométriques de proportion en nous appuyant sur l’équilibre, mais nous aurions également pu le mettre en lumière en utilisant la résistance à la flexion des encorbellements. Ungewitter indique qu’il n’est pas possible de donner de rapport de proportion général entre la hauteur et la saillie, car ce rapport dépend de la charge portée par le corbeau. Pour une même saillie, plus la charge sera importante, plus la hauteur du corbeau doit être importante. Il donne néanmoins des ordres de grandeur : « le rapport entre la saillie et la hauteur est compris généralement entre 1/1 et 1/2, et parfois même moins que 1/2 » (1901 [16, p.240] 1920 [17, p.334]). Règlements anciens Suite à une série d’accidents avec chute d’entablements et corniches, des règlements imposent à Paris à partir de 1712 que les pierres de taille qui les composent fassent parpaing, c’est à dire que leur queue fasse l’épaisseur complète du mur. Cette préconisation sera rappelée régulièrement dans des ordonnances successives (1712, 1721, 1823). Cette règle forfaitaire ne fixe cependant pas de limite à la saillie à donner aux encorbellements. On peut noter que les exemples de calcul présentés par Ungewitter et Mohrmann ne repectent pas du tout cette prescription (1901 [16, p.239-240]).4.2 Règles de dimensionnement
On reprend les mêmes notations que dans la partie consacrée à l’équilibre et à la résistance ci-dessus. De plus, on note $\sigo $ la résistance admissible à la flexion. Il est à noter que le terme de résistance admissible renvoie à des valeurs différentes suivant les époques et les auteurs. Ungewitter et Mohrmann – Lehrbuch der gotischen Konstruktionen Nous avons vu plus haut le mode de dimensionnement de Ungewitter et Mohrmann, qui vérifient à la fois l’équilibre, et la résistance en flexion et en cisaillement. Les contraintes admissibles indiquées par ces auteurs sont les suivantes. Pour la flexion6, Ungewitter et Mohrmann considèrent comme admissible une contrainte comprise entre 2 et 10 kg/cm2. Pour le cisaillement, Ungewitter et Mohrmann considèrent comme admissible7 des contraintes de 1,5 à 4 kg/cm2 pour le grès et les briques, de 3 à 6 kg/cm2 pour le calcaire et de 5 à 10 kg/cm2 pour le granite (1901 [16, p.239-240] 1920 [17, p.332-334]). Ces contraintes correspondent à un mode de calcul où la contrainte de cisaillement est uniforme, donc dans le cas d’une section rectangulaire $\tau = Q/bh$. De plus, ils donnent une règle de prédimensionnement pour les corbeaux : « pour les corbeaux en matériau de qualité modérée, dont la saillie n’excède pas la hauteur, doivent avoir une section dans le plan du mur avec une aire en cm2 égale à la charge en kg. » (1901 [16, p.240] 1920 [17, p.333]) Planat – Pratique de la mécanique appliquée à la résistance des matériaux La méthode de dimensionnement des consoles de balcon de Planat à la fin du XIXe siècle est équivalente à celle de Ungewitter et Mohrmann, à ceci près que la résistance en cisaillement et compression sont négligées. Dans son premier exemple, Planat se place dans le cas où il est nécessaire de déterminer la hauteur minimale à donner à la console. La formule qu’il obtient pour le respect du critère de flexion est ([13,p.189]) : \begin{equation} h=\sqrt{\frac{6mQ}{\sigo b}} \end{equation} Cette formule est équivalente au mode de dimensionnement donné dans la première partie de cet article. Dans son second exemple, Planat indique que les consoles considérées font toute l’épaisseur du mur ([13,p.194]). Il considère que la dalle du balcon inférieur porte entre les consoles, mais vérifie également qu’il est possible d’encastrer la dalle dans le mur de façade. Il semble que Planat dimensionne en flexion les consoles inférieures comme si ces dernières étaient monolithes ($h$=1m30 p.193), alors que le dessin p.190 semble montrer des consoles composées de deux assises. Peut-être considère-t-il que le calcul de la contrainte de flexion n’est qu’estimatif et qu’il n’est pas nécessaire de distinguer les différentes assises de la console, cependant ce point n’est pas précisé. Planat donne une synthèse des résultats d’expérience concernant la résistance à la compression des calcaires, grès, meulières, schistes etc. Il indique ensuite un rapport de 0,133 entre la résistance à l’extension (résistance à la traction) et celle à la compression, tout en soulignant le manque de valeurs sur cette question, et donc le peu de fiabilité du rapport de 0,133 qu’il propose, et qui n’est valable que pour les calcaires ([13,p.85]). Il utilise un coefficient de sécurité de 1/10 dans ses exemples ([13,pp.189,190]). Pour finir, mentionnons les caractéristiques des pierres des exemples de Planat :- console en pierre pp.188-189 calcaire: résistance à la compression de 225kg/cm2, résistance à la traction de 0,133×225=30kg/cm2, à laquelle il applique un coefficient de sécurité de 1/10
- balcon en pierre pp.189-193:
- grès : poids 2600kg/m3, résistance à la compression de 500kg/cm2, résistance à la traction de 160kg/cm2, auxquelles il applique un coefficient de sécurité de 1/10
- pierre de Jaumont : poids 2300 à 2400kg/m3, résistance à la compression de 165kg/cm2, résistance à la traction de 30 à 40kg/cm2, auxquelles il applique un coefficient de sécurité de 1/10
5 Conclusion
Cette présentation de la stabilité des encorbellement montre l’importance de la queue des corbeaux et des consoles, ainsi que de leurs contrepoids, éventuellement fixés à l’aide d’éléments métalliques. Une des difficultés pour bien appréhender l’équilibre de ces encorbellements est l’absence de références visuelles concernant leur équilibre. La queue des consoles et corbeaux ne sont pas visibles, pas plus que les éléments métalliques pour la fixation des contrepoids. Sur les dessins et plans anciens, elles ne sont pas souvent représentées, tout simplement car la longueur de cette dernière n’est pas connue, ou n’intéresse pas pour le sujet traité par le dessinateur9. Cet article sera suivi dans le futur de deux articles traitant des balcons et des corniches.Article mis en ligne le : 23/11/2014.
Sur l’auteur :
Mathias Fantin est ingénieur structure et docteur en architecture, et il travaille sur la restauration des monuments anciens. Il a fondé en 2014 Bestrema, un bureau d’études structures spécialisé dans ce domaine. Ces autres articles pourraient également vous intéresser :- Résistance et stabilité des remplages -
 Vérification de la résistance et stabilité des remplages, supports en pierre des vitraux dans les édifices gothiques.
Vérification de la résistance et stabilité des remplages, supports en pierre des vitraux dans les édifices gothiques. - La géométrie des voûtes -
 La géométrie des voûtes renvoie à deux concepts : la forme de l’intrados et l’appareil. Étude des correspondances et divergences entre les deux.
La géométrie des voûtes renvoie à deux concepts : la forme de l’intrados et l’appareil. Étude des correspondances et divergences entre les deux. - Étude des rapports entre stéréotomie et … -
 Présentation d’une thèse de doctorat en architecture explorant l’influence de la coupe des pierres sur la stabilité des voûtes clavées.
Présentation d’une thèse de doctorat en architecture explorant l’influence de la coupe des pierres sur la stabilité des voûtes clavées.
Bibliographie
- [1]
- J.-P. ADAM : La construction romaine : matériaux et techniques. Picard, Paris, 1989.
- [2]
- ASSOCIATION OUVRIèRE DES COMPAGNONS DU DEVOIR FRANCE : La maçonnerie et la pierre de taille, vol. 6 de Encyclopédie des métiers. Librairie du Compagnonnage, Paris, 1991.
- [3]
- B. CHARUE, J. FREDET, O. LEMOINE et J.-L. TAUPIN : Guide du diagnostic des structures. Agence National pour l’Amélioration de l’Habitat, Paris, 2e édn, 1984.
http://www.ceacap.org/dokuwiki/doku.php/habitat_ancien_parisien?DokuWiki=8b82ea81d85dffabe4f71916907e2207 - [4]
- A. CHOISY : Histoire de l’architecture, vol. 2. Gauthier-Villars, Paris, 1899.
http://www.augustechoisy2009.net/ - [5]
- A. CHOISY : Histoire de l’architecture, vol. 1. Gauthier-Villars, Paris, 1899.
http://www.augustechoisy2009.net/ - [6]
- J. CLAUDEL et L. LAROQUE : Pratique de l’art de construire – Maçonnerie. Carilian-Goeury et V. Dalmont, Paris, 1850.
http://www.google.fr/books?id=zygOb89Ro1MC - [7]
- A.-C. D’AVILER : Cours d’architecture qui comprend les ordres de Vignole. Nicolas Langlois, Paris, 1691.
http://architectura.cesr.univ-tours.fr/Traite/Notice/ENSBA_LES223.asp?param= - [8]
- N. DE LA MARE : Traité de la police, vol. 4. J.-F. Hérissant, Paris, 1738.
http://gallica.bnf.fr/ark:/12148/bpt6k109901t - [9]
- J. P. DOULIOT : Traité spécial de coupe des pierres. Carilian-Goeury, Paris, 1825.
http://books.google.fr/books?id=BqUJAAAAIAAJ - [10]
- C. ENLART : Manuel d’archéologie française depuis les temps mérovingiens jusqu’à la Renaissance – I. Architecture religieuse Tome 1. Auguste Picard, Paris, 3e édn, 1927.
http://gallica.bnf.fr/ark:/12148/bpt6k364918 - [11]
- S. HUERTA FERNáNDEZ : Geometry and equilibrium: The gothic theory of structural design. Structural Engineer, 84(2): 23-28, 2006.
http://oa.upm.es/701/ - [12]
- P. PATTE : Mémoires sur les objets les plus importans de l’architecture. Rozet, Paris, 1769.
http://gallica.bnf.fr/ark:/12148/bpt6k5701519t - [13]
- P. PLANAT : Pratique de la mécanique appliquée à la résistance des matériaux. Aulanier, Paris, 5e édn.
http://gallica.bnf.fr/ark:/12148/bpt6k207198r - [14]
- P. PLANAT : Corniche. Encyclopédie de l’architecture et de la construction – Volume IV, partie 1 : CO – ES, 1888.
http://www.purl.org/yoolib/inha/8431 - [15]
- C.-J. TOUSSAINT : Manuel d’architecture, ou traité de l’art de batir – Tome 1. Roret, Paris, 1828.
http://gallica.bnf.fr/ark:/12148/bpt6k63737162 - [16]
- G. G. UNGEWITTER et K. MOHRMANN : Lehrbuch der gotischen Konstruktionen, vol. 1. Tauchnitz, Leipzig, 4e édn, 1901.
http://books.google.fr/books?id=SksAAAAAYAAJ - [17]
- G. G. UNGEWITTER et K. MOHRMANN : Manual of Gothic Construction – Third Edition. Traduction N. C. RICKER. Illinois, 1920.
http://archive.org/details/5631513 - [18]
- VERNIS : Elargissement des anciens ponts par encorbellement – Ponts de Seurre et de Clerval. Annales des ponts et chaussées, 1876.
http://gallica.bnf.fr/ark:/12148/cb34348188q/date - [19]
- E. VIOLLET–LE-DUC : Corniche. Dictionnaire raisonné de l’architecture française du XIe au XVIe siècle, 1860.
http://fr.wikisource.org/wiki/Dictionnaire_raisonn%C3%A9_de_l%E2%80%99architecture_fran%C3%A7aise_du_XIe_au_XVIe_si%C3%A8cle/Corniche
Notes :
1 Cette définition de la contrainte de cisaillement suppose que cette dernière est uniforme dans la section, ce qui est contestable. Nous pourrions utiliser une autre définition, par exemple $\tau = 3Q / \left (2bh\right )$ prenant en compte la non uniformité de la contrainte. Cependant comme nous utiliserons dans la suite les résistances données par des auteurs anciens, nous conservons leur définition, afin de permettre la comparaison.
2 Ce point se démontre en considérant l’égalité des contraintes lorsque les deux modes de rupture sont équivalents : ${{Q}\over{bh}}={{6mQ}\over{bh^2}}$
3 « From safety in calculation the point $d$ is not taken at the face of the wall, but a few cm farther back toward $d’$ » Ungewitter 1901 [16,p.239] 1920 [17,p.332]
4 Voir Ungewitter 1901 [16,p.239] 1920 [17,p.332] et 1901 [16,p.240] 1920 [17,p.334].
5
Par exemple, Choisy écrit dans l’histoire de l’architecture :
- à propos de la corniche du palais Strozzi : « l’équilibre de ces masses proéminentes ne pouvait s’obtenir qu’au prix d’élégissements intérieurs, de contrepoids plus ou moins habilement combinés » [4,p.627]
- concernant les corniches romanes : « La corniche se réduit ainsi à un encorbellement : pour permettre de lui donner une forte saillie, on l’élégit en chanfrein, quelquefois modillonnée ; ou bien on la construit à l’aide d’une rangée de corbeaux soutenant une tablette de couronnement ; on sculpte les modillons et l’on profile la tablette » [4,p. 172-173]. L’élégissement en chanfrein correspond ici à un amaigrissement du profil.
- concernant les corniches ioniques de l’architecture grecque : « Le rôle utile des denticules est de former un encorbellement élégi qui permet d’exagérer la saillie de la corniche et par suite de mieux abriter la façade » [5,p.364].